题目内容
8.已知数列{an},其前n项和为${S_n}=\frac{3}{2}{n^2}+\frac{7}{2}n\;(n∈{N^*})$.(Ⅰ)求数列{an}的通项公式,并证明数列{an}是等差数列;
(Ⅱ)若数列{bn}满足${b_n}={2^{{a_n}-2}}$,求数列{bn}的通项公式,并证明数列{bn}是等比数列;
(Ⅲ)若数列{cn}满足${c_n}={a_n}•{b_n}^{\frac{1}{3}}$,求数列{cn}的前n项和Tn.
分析 (Ⅰ)运用数列的通项和前n项和的关系,化简整理可得{an}的通项公式,再由定义即可得到证明;
(Ⅱ)求得{bn}的通项公式,再由定义可证为等比数列;
(Ⅲ)求得数列{cn}的通项公式,再由数列的求和方法:错位相减法,结合等比数列的求和公式,计算即可得到所求和.
解答 解:(Ⅰ)${S_n}=\frac{3}{2}{n^2}+\frac{7}{2}n\;(n∈{N^*})$.
当n=1时,a1=5,
当n≥2时,an=Sn-Sn-1=$\frac{3}{2}$[n2-(n-1)2]+$\frac{7}{2}$[n-(n-1)]=3n+2,
又a1=5满足an=3n+2,则an=3n+2.
∵an-an-1=3n+2-[3(n-1)+2]=3(n≥2,n∈N),
∴数列{an}是以5为首项,3为公差的等差数列.
(Ⅱ)由已知得${b_n}={2^{{a_n}-2}}$=8n,
∵$\frac{{b{\;}_{n+1}}}{b_n}=8,(n∈{N^*})$,
则数列{bn}是以8为首项,8为公比的等比数列.
(Ⅲ)${c_n}={a_n}•{b_n}^{\frac{1}{3}}=(3n+2)•{2^n}$,
前n项和Tn=5•2+8•22+11•23+…+(3n+2)•2n,
2Tn=5•22+8•23+11•24+…+(3n+2)•2n+1,
两式相减可得,-Tn=10+3(22+23+…+2n)-(3n+2)•2n+1
=10+3•$\frac{4(1-{2}^{n-1})}{1-2}$-(3n+2)•2n+1,
化简可得Tn=(3n-1)•2n+1+2.
点评 本题考查等差数列和等比数列的定义和通项公式,考查数列的求和方法:错位相减法,同时考查等比数列的求和公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知0<a<b,且a+b=1,则下列不等式中,正确的是( )
| A. | log2a>0 | B. | 2a-b$<\frac{1}{2}$ | C. | log2a+log2b<-2 | D. | 2${\;}^{\frac{b}{a}+\frac{a}{b}}$$<\frac{1}{2}$ |
19.一次函数f(x)的图象过点A(0,3)和B(4,1),则f(x)的单调性为( )
| A. | 增函数 | B. | 减函数 | C. | 先减后增 | D. | 先增后减 |
16.如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为( )
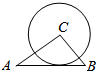

| A. | 2.3 | B. | 2.4 | C. | 2.5 | D. | 2.6 |
3.已知命题p:?x∈R,3x>2x;命题q:?x∈R,tanx=2,则下列命题为真命题的是( )
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
17.下列说法中,正确的是( )
| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 根据样本估计总体,其误差与所选择的样本容量无关 | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |