题目内容
【题目】在![]() 中,内角
中,内角![]() 的对边分别是
的对边分别是![]() ,已知
,已知![]() 为锐角,且
为锐角,且![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)设函数![]() ,其图象上相邻两条对称轴间的距离为
,其图象上相邻两条对称轴间的距离为![]() .将函数
.将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 上的值域.
上的值域.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)由正弦定理可得: ![]()
由于![]() ,利用两角和的正弦函数公式可求
,利用两角和的正弦函数公式可求![]() 的值,结合
的值,结合![]() 的范围即可得解
的范围即可得解![]() 的值.
的值.
(Ⅱ)利用三角函数恒等变换的应用化简函数解析式可得![]()
,由已知可求![]() ,利用周期公式可求
,利用周期公式可求![]() ,利用三角函数平移变换可求
,利用三角函数平移变换可求![]()
,由![]() 的范围,利用正弦函数的性质可求
的范围,利用正弦函数的性质可求![]() 的值域.
的值域.
试题解析:(Ⅰ)∵![]() ,
,
∴由正弦定理得: ![]() ,
,
∴![]() 为锐角,
为锐角, ![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
即![]() ,
,
∴![]() .
.
(Ⅱ)由(Ⅰ)得![]() ,
,
∵![]() 的图象相邻两对称轴间的距离为
的图象相邻两对称轴间的距离为![]() ,
,
∴![]() ,得
,得![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴函数![]() 在
在![]() 上的值域为
上的值域为![]() .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
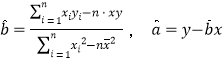 .
.