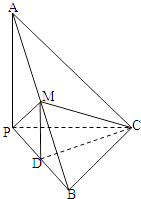
题目内容
【题目】已知动圆![]() 过定点
过定点![]()
![]() ,且与定直线
,且与定直线![]() 相切,动圆圆心
相切,动圆圆心![]() 的轨迹方程为
的轨迹方程为![]() ,直线
,直线![]() 过点
过点![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)若![]() 交
交![]() 轴于点
轴于点![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,在
,在![]() 上是否存在点
上是否存在点![]() 使
使![]() 为正三角形?若能,求点
为正三角形?若能,求点![]() 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
【答案】(1) ![]() (2) 直线l上不存在点E,使得△ABE是正三角形.
(2) 直线l上不存在点E,使得△ABE是正三角形.
【解析】试题分析:
(1)由题意可知曲线C是抛物线,可得抛物线方程,把直线方程代入抛物线方程得x的一元二次方程,同时设设![]() ,利用韦达定理得
,利用韦达定理得![]() ,用坐标表示出
,用坐标表示出![]() ,利用基本不等式并转化为
,利用基本不等式并转化为![]() ,代入韦达定理的结论可得.
,代入韦达定理的结论可得.
(2)假设存在点![]() ,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB|, 由抛物线定义知
,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB|, 由抛物线定义知![]() ,这样把|BE|=
,这样把|BE|= ![]() 和|AE|=
和|AE|= ![]() 用坐标表示,两式相减就可解得
用坐标表示,两式相减就可解得![]() ,从而得E点坐标,但检验发现此时
,从而得E点坐标,但检验发现此时![]() ,故刚才的解不正确,即不存在E点满足题意.
,故刚才的解不正确,即不存在E点满足题意.
试题解析:
(1)依题意,曲线C是以点P为焦点,直线![]() 为准线的抛物线,
为准线的抛物线,
所以曲线C的方程为![]()
设![]() 方程为
方程为![]() 代入
代入![]() 由消去
由消去![]() 得
得![]()
设![]() 、
、![]() ,则
,则![]()
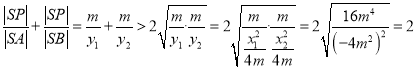
所以![]() 的取值范围是
的取值范围是![]()
(2)由(1)知![]() 方程为
方程为![]() 代入
代入![]() 由消去
由消去![]() 得
得![]()
![]() ,
, 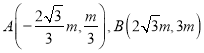
假设存在点![]() ,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB|,
,使△ABE为正三角形,则|BE|=|AB|且|AE|=|AB|,
![]() 即
即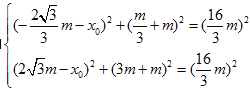 ,
, ![]() .
.
若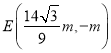 ,则
,则![]()
因此,直线l上不存在点E,使得△ABE是正三角形.
解法二:设AB的中点为G,则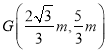
由![]() 联立
联立![]() 方程
方程
 与
与![]() 方程求得
方程求得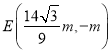
由![]() 得
得![]() ,矛盾
,矛盾
因此,直线l上不存在点E,使得△ABE是正三角形.

练习册系列答案
相关题目