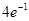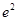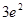题目内容
设函数
(1)当 时,求曲线
时,求曲线 处的切线方程;
处的切线方程;
(2)当 时,求
时,求 的极大值和极小值;
的极大值和极小值;
(3)若函数 在区间
在区间 上是增函数,求实数
上是增函数,求实数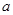 的取值范围.
的取值范围.

(1)当
 时,求曲线
时,求曲线 处的切线方程;
处的切线方程;(2)当
 时,求
时,求 的极大值和极小值;
的极大值和极小值;(3)若函数
 在区间
在区间 上是增函数,求实数
上是增函数,求实数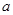 的取值范围.
的取值范围.(1)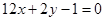
(2) 的极大值为
的极大值为
(3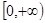
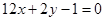
(2)
 的极大值为
的极大值为
(3
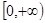
(1)中,先利用 ,表示出点
,表示出点 的斜率值
的斜率值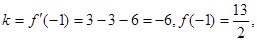 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当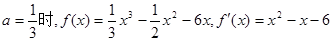 ,再令
,再令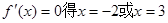 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。
解:(1)当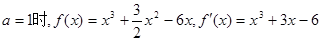 ……2分
……2分
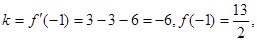 ∴
∴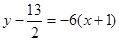
即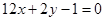 为所求切线方程。………………4分
为所求切线方程。………………4分
(2)当
令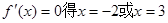 ………………6分
………………6分
∴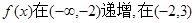 递减,在(3,+
递减,在(3,+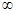 )递增
)递增
∴ 的极大值为
的极大值为 …………8分
…………8分
(3)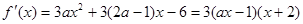
①若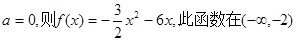 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分
②若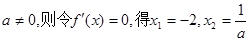
∵ 恒成立,
恒成立,
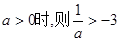 恒成立,即a>0……………11分
恒成立,即a>0……………11分
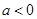 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数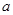 的取值范围是
的取值范围是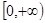
 ,表示出点
,表示出点 的斜率值
的斜率值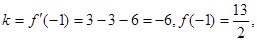 这样可以得到切线方程。(2)中,当
这样可以得到切线方程。(2)中,当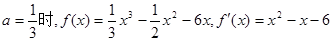 ,再令
,再令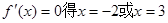 ,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了
,利用导数的正负确定单调性,进而得到极值。(3)中,利用函数在给定区间递增,说明了 在区间
在区间 导数恒大于等于零,分离参数求解范围的思想。
导数恒大于等于零,分离参数求解范围的思想。解:(1)当
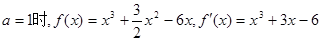 ……2分
……2分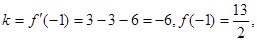 ∴
∴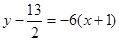
即
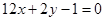 为所求切线方程。………………4分
为所求切线方程。………………4分(2)当

令
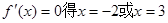 ………………6分
………………6分∴
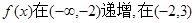 递减,在(3,+
递减,在(3,+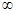 )递增
)递增∴
 的极大值为
的极大值为 …………8分
…………8分(3)
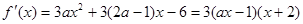
①若
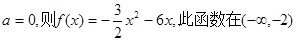 上单调递增。∴满足要求。…10分
上单调递增。∴满足要求。…10分②若
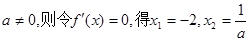
∵
 恒成立,
恒成立,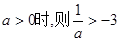 恒成立,即a>0……………11分
恒成立,即a>0……………11分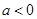 时,不合题意。综上所述,实数
时,不合题意。综上所述,实数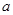 的取值范围是
的取值范围是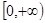

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
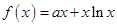 的图象在点
的图象在点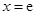 (
(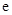 为自然对数的底数)处的切线斜率为3.
为自然对数的底数)处的切线斜率为3.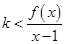 (Ⅰ)求实数
(Ⅰ)求实数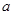 的值;
的值;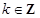 ,且 对任意
,且 对任意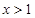 恒成立,求
恒成立,求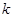 的最大值;
的最大值;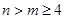 时,证明
时,证明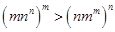 .
.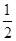 x2
x2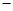 ㏑x的单调递减区间为
㏑x的单调递减区间为 1,1]
1,1]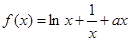 (
(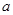 为实数).
为实数).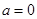 时, 求
时, 求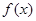 的最小值;
的最小值;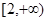 上是单调函数,求
上是单调函数,求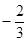 与x=1时都取得极值.
与x=1时都取得极值.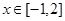 ,不等式f(x)<c2恒成立,求c的取值范围.
,不等式f(x)<c2恒成立,求c的取值范围.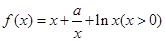 ,其中
,其中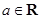 .
.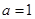 时,求
时,求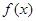 的单调递增区间;
的单调递增区间;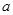 的取值范围,使得对任意的
的取值范围,使得对任意的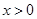 ,都有
,都有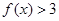 .
.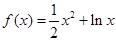 .
.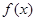 在区间
在区间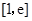 上的最大、最小值;
上的最大、最小值;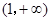 上,函数
上,函数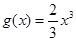 的图象的下方
的图象的下方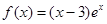 的单调递增区间是 ( )
的单调递增区间是 ( ) 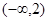
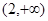
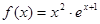 ,
,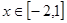 的最大值为
的最大值为