题目内容
如图,已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则异面直线PA与BC所成的角为________.

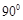
本试题主要是考查了四面体中异面直线的所成的角的求解问题。
因为已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则点P在底面的射影落在CB的中点D,因此PD垂直于平面ABC,然后BC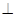 垂直于AD,BC
垂直于AD,BC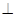 PD,得到BC
PD,得到BC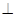 平面PAD,利用线面垂直的性质定理可知异面直线PA与BC所成的角为
平面PAD,利用线面垂直的性质定理可知异面直线PA与BC所成的角为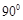 。故答案为
。故答案为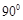 。
。
解决该试题的关键是能理解四面体中,点P在底面的射影落在CB的中点位置上,得到BC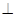 平面PAD。
平面PAD。
因为已知四面体P-ABC中,PA=PB=PC,且AB=AC,∠BAC=90°,则点P在底面的射影落在CB的中点D,因此PD垂直于平面ABC,然后BC
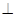 垂直于AD,BC
垂直于AD,BC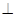 PD,得到BC
PD,得到BC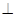 平面PAD,利用线面垂直的性质定理可知异面直线PA与BC所成的角为
平面PAD,利用线面垂直的性质定理可知异面直线PA与BC所成的角为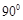 。故答案为
。故答案为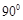 。
。解决该试题的关键是能理解四面体中,点P在底面的射影落在CB的中点位置上,得到BC
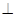 平面PAD。
平面PAD。
练习册系列答案
相关题目
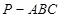 中,
中,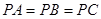 ,底面
,底面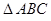 是正三角形,
是正三角形,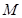 、
、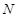 分别是侧棱
分别是侧棱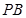 、
、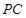 的中点. 若平面
的中点. 若平面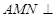 平面
平面 ,则侧棱
,则侧棱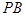 与平面
与平面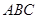 所成角的正切值是( )
所成角的正切值是( )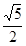
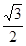
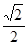
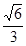
 中,
中,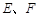 分别为
分别为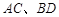 的中点,若
的中点,若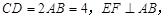 则
则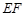 与
与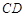 所成的角为
所成的角为



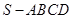 的侧棱长为
的侧棱长为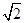 ,底面边长为
,底面边长为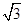 ,
,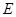 为
为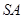 中点,则异面直线
中点,则异面直线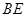 与
与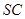 所成的角是 .
所成的角是 .
 的正方形
的正方形 沿对角线
沿对角线 成直二面角(平面
成直二面角(平面 平面
平面 ),则
),则 的度数是( )
的度数是( ) B.
B.  C.
C.  D
D 




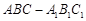 中已知
中已知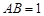 ,
,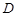 在棱
在棱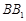 上,且
上,且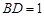 ,若
,若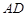 与平面
与平面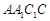 所成的角为
所成的角为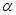 ,则
,则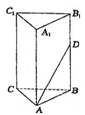




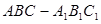 中,
中, 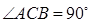 ,
,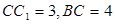 ,
, 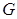 是
是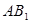 和
和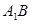 的交点, 若
的交点, 若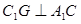 .
. 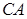 的长; (2)求点
的长; (2)求点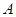 到平面
到平面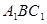 的距离;
的距离;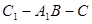 的平面角的正弦值的大小.
的平面角的正弦值的大小.