题目内容
(2012•芜湖二模)定义在R上的偶函数f (x)满足f (2-x)=f(x),且在[-3,-2]上是减函数,α,β是钝角三角形的两个锐角,则下列结论正确的是( )
分析:先确定函数的周期,再确定函数的单调性,即可求得结论.
解答:解:∵f(2-x)=f(x),∴f(x+2)=f(-x)=f(x),∴T=2
∵f(x)在[-3,-2]上是减函数,∴在[-1,0]上是减函数,
∵函数是偶函数,∴在[0,1]上是增函数
∵α,β是钝角三角形的两个锐角,∴0<α+β<
∴0<α<
-β<
,
∴0<sinα<sin(
-β)=cosβ<1
∴f(sinα)<f(cosβ)
故选B.
∵f(x)在[-3,-2]上是减函数,∴在[-1,0]上是减函数,
∵函数是偶函数,∴在[0,1]上是增函数
∵α,β是钝角三角形的两个锐角,∴0<α+β<
| π |
| 2 |
∴0<α<
| π |
| 2 |
| π |
| 2 |
∴0<sinα<sin(
| π |
| 2 |
∴f(sinα)<f(cosβ)
故选B.
点评:本题考查函数单调性与奇偶性的综合,考查函数的周期性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
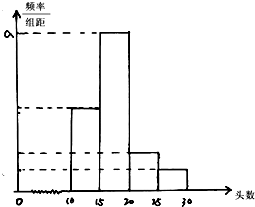 (2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下:
(2012•芜湖二模)某省对省内养殖场“瘦肉精”使用情况进行检查,在全省的养殖场随机抽取M个养殖场的猪作为样本,得到M个养殖场“瘦肉精”检测阳性猪的头数,根据此数据作出了频率分布表和频率分布直方图如下: