题目内容
在数列{an}中,如果对任意n∈N*都有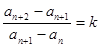 (k为常数),则称{an}为等差比数列,k称为公差比.现给出下列命题:
(k为常数),则称{an}为等差比数列,k称为公差比.现给出下列命题:
(1)等差比数列的公差比一定不为0;
(2)等差数列一定是等差比数列;
(3)若an=-3n+2,则数列{an}是等差比数列;
(4)若等比数列是等差比数列,则其公比等于公差比.
其中正确的命题的序号为________.
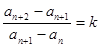 (k为常数),则称{an}为等差比数列,k称为公差比.现给出下列命题:
(k为常数),则称{an}为等差比数列,k称为公差比.现给出下列命题:(1)等差比数列的公差比一定不为0;
(2)等差数列一定是等差比数列;
(3)若an=-3n+2,则数列{an}是等差比数列;
(4)若等比数列是等差比数列,则其公比等于公差比.
其中正确的命题的序号为________.
(1) (3) (4)
解:(1)若公差比为0,则an+2-an+1=0,故{an}为常数列,从而an+2-an+1 an+1-an =k的分母为0,无意义,所以公差比一定不为零;
(2)当等差数列为常数列时,不能满足题意;
(3)若an=-3n+2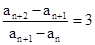 是公差比为3的等差比数列;
是公差比为3的等差比数列;
(4)an=a1•qn-12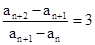 命题正确,所以,正确命题为(1)(3)(4).
命题正确,所以,正确命题为(1)(3)(4).
故答案为(1)(3)(4)
(2)当等差数列为常数列时,不能满足题意;
(3)若an=-3n+2
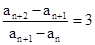 是公差比为3的等差比数列;
是公差比为3的等差比数列;(4)an=a1•qn-12
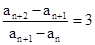 命题正确,所以,正确命题为(1)(3)(4).
命题正确,所以,正确命题为(1)(3)(4).故答案为(1)(3)(4)

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
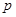 :曲线
:曲线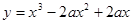 上任一点处的切线的倾斜角都是锐角;命题
上任一点处的切线的倾斜角都是锐角;命题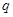 :直线
:直线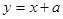 与曲线
与曲线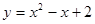 有两个不同的公共点;若命题
有两个不同的公共点;若命题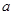 的取值范围.
的取值范围. ,使
,使
 ,
, 


 ,则
,则 为:
为: .
.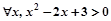 ”的否命题是“
”的否命题是“ ”.
”. 则q”的逆否命题是“若p,则
则q”的逆否命题是“若p,则 ”.
”. 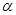 ,使
,使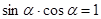 ;
;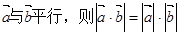
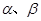 是第一象限的角,且
是第一象限的角,且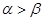 ,则
,则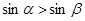
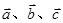 是任意的非零向量,且相互不共线,
是任意的非零向量,且相互不共线,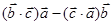 与
与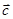 垂直;
垂直;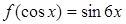 ,则
,则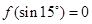 .
.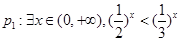 ;
;  ㏒1/2x>㏒1/3x
㏒1/2x>㏒1/3x ㏒1/2x ;
㏒1/2x ;  ㏒1/3x 其中的真命题是 ( )
㏒1/3x 其中的真命题是 ( ) (
(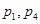


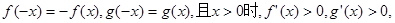 则
则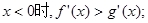
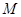 在平面
在平面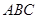 内,并且对空间任一点
内,并且对空间任一点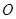 ,
,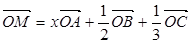 ,则
,则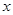 的值为1;
的值为1; 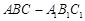 中,若
中,若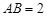 ,
,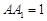 ,则点
,则点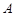 到平面
到平面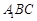 的距离为
的距离为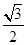 ,其中正确命题的序号是
,其中正确命题的序号是 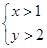 是
是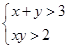 的充要条件;
的充要条件;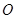 ,若满足
,若满足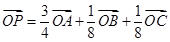 ,则
,则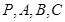 四点一定共面.
四点一定共面.