Question

（2012•淮北二模）已知圆C：x²+y²=1，过点P（0，2）作圆C的切线，交x轴正半轴于点Q、若M（m，n）为线段PQ上的动点，则

3

m

+

1

n

的最小值为

4

．

Answer 1

分析：根据题意画出相应的图形，连接CN，由PQ与圆C相切，利用切线的性质得到CN垂直于PQ，且CN等于圆C半径，可得出CN为CP的一半，得到∠CPQ为30°，进而求出直线PQ的斜率，确定出直线PQ的解析式，由M为直线PQ上的点，将M（m，n）代入直线方程，用m表示出n，将所求式子利用基本不等式变形后，得到取等号时m与n的关系，将表示出的n代入求出m的值，进而得到n的值，即可确定出所求式子的最小值．

解答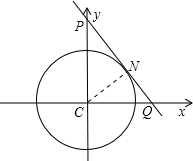：解：根据题意画出相应的图形，如图所示：
连接CN，
∵PQ与圆C相切，
∴CN⊥PQ，且CN=1，
又P（0，2），即CP=2，
∴在Rt△PCN中，CN=

1

2

PC，
∴∠CPN=30°，
∴直线PQ的倾斜角为120°，即斜率k=-

3

，
故直线PQ解析式为y=-

3

x+2，
∴M（m，-

3

m+2），
又

3

m

+

1

n

≥2

3 mn

，当且仅当

3

m

=

1

n

，即m=

3

n时取等号，
∴m=

3

（-

3

m+2）=-3m+2

3

，即m=

3

2

，n=

1

2

，
则

3

m

+

1

n

的最小值为2

3 3 2 × 1 2

=4．
故答案为：4

点评：此题考查了直线与圆的位置关系，以及基本不等式的应用，涉及的知识有：切线的性质，含30°直角三角形的性质，直线倾斜角与斜率的关系，以及坐标与图形性质，当直线与圆相切时，圆心到直线的距离等于圆的半径，且切线垂直于过切点的半径，熟练掌握此性质是解本题的关键．