题目内容
如图,已知△ABC的顶点为A(2,4),B(0,-2),C(-2,3),求:
(Ⅰ)AB边所在直线的方程;
(Ⅱ)AB边上的高线CH所在直线的方程.

(Ⅰ)AB边所在直线的方程;
(Ⅱ)AB边上的高线CH所在直线的方程.

(1)∵A(2,4),B(0,-2),
∴kAB=
=3,
由点斜式方程可得y-(-2)=3(x-0),
化为一般式可得3x-y-2=0
(2)由(1)可知kAB=3,
故AB边上的高线CH所在直线的斜率为-
,
又AB边上的高线CH所在直线的过点C(-2,3),
所以方程为y-3=-
(x+2),
化为一般式可得x+3y-7=0
∴kAB=
| 4-(-2) |
| 2-0 |
由点斜式方程可得y-(-2)=3(x-0),
化为一般式可得3x-y-2=0
(2)由(1)可知kAB=3,
故AB边上的高线CH所在直线的斜率为-
| 1 |
| 3 |
又AB边上的高线CH所在直线的过点C(-2,3),
所以方程为y-3=-
| 1 |
| 3 |
化为一般式可得x+3y-7=0

练习册系列答案
相关题目
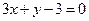 与
与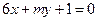 平行,则它们之间的距离为( )
平行,则它们之间的距离为( )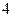
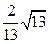
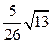
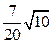
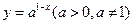 的图像恒过定点
的图像恒过定点 ,若点
,若点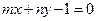
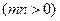 上,则
上,则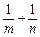 的最小值为 .
的最小值为 .