题目内容
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.(1)试确定m,使直线AP与平面BDD1B1所成角的正切值为3
| 2 |
(2)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,并证明你的结论.
分析:(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点,连接OG,证明AO⊥平面BDD1B1,说明∠AGO是AP与平面BDD1B1所成的角.在Rt△AOG中,利用直线AP与平面BDD1B1所成的角的正切值为3
.求出m的值.
(2)点Q应当是AICI的中点,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,通过证明 D1O1⊥平面ACC1A1,D1O1⊥AP.利用三垂线定理推出结论.
| 2 |
(2)点Q应当是AICI的中点,使得对任意的m,D1Q在平面APD1上的射影垂直于AP,通过证明 D1O1⊥平面ACC1A1,D1O1⊥AP.利用三垂线定理推出结论.
解答: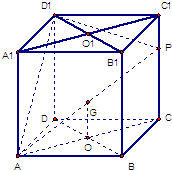 解:(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点G,
解:(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点G,
连接OG,因为PC∥平面BDD1B1,平面BDD1B1∩平面APC=OG,
故OG∥PC,所以,OG=
PC=
.
又AO⊥BD,AO⊥BB1,所以AO⊥平面BDD1B1,
故∠AGO是AP与平面BDD1B1所成的角.
在Rt△AOG中,tan∠AGO=
=
=3
,即m=
.
所以,当m=
时,直线AP与平面BDD1B1所成的角的正切值为3
.
(2)可以推测,点Q应当是AICI的中点,当是中点时
因为D1O1⊥A1C1,且 D1O1⊥A1A,A1C1∩A1A=A1,
所以 D1O1⊥平面ACC1A1,
又AP?平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直.
 解:(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点G,
解:(1)连AC,设AC与BD相交于点O,AP与平面BDD1B1相交于点G,连接OG,因为PC∥平面BDD1B1,平面BDD1B1∩平面APC=OG,
故OG∥PC,所以,OG=
| 1 |
| 2 |
| m |
| 2 |
又AO⊥BD,AO⊥BB1,所以AO⊥平面BDD1B1,
故∠AGO是AP与平面BDD1B1所成的角.
在Rt△AOG中,tan∠AGO=
| OA |
| GO |
| ||||
|
| 2 |
| 1 |
| 3 |
所以,当m=
| 1 |
| 3 |
| 2 |
(2)可以推测,点Q应当是AICI的中点,当是中点时
因为D1O1⊥A1C1,且 D1O1⊥A1A,A1C1∩A1A=A1,
所以 D1O1⊥平面ACC1A1,
又AP?平面ACC1A1,故 D1O1⊥AP.
那么根据三垂线定理知,D1O1在平面APD1的射影与AP垂直.
点评:本题考查直线与平面所成的角,考查直线与平面垂直的判定,三垂线定理的应用,考查空间想象能力,逻辑推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
 如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
