题目内容
某人上午7时,乘摩托艇以匀速v n mile/h(4≤v≤20)从A港出发到距50 n mile的B港去,然后乘汽车以匀速w km/h(30≤w≤100)自B港向距300 km的C市驶去.应该在同一天下午4至9点到达C市.设乘汽车、摩托艇去所需要的时间分别是x h、y h.(1)作图表示满足上述条件的x、y范围;
(2)如果已知所需的经费p=100+3×(5-x)+2×(8-y)(元),那么v、w分别是多少时走得最经济?此时需花费多少元?
分析:(1)要作出满足条件的x,y的范围,要先分析题意,找出相关量之间的不等关系,即x,y满足的约束条件,由约束条件画出可行域;
(2)要求花费的最小值,即求可行域中的最优解,在线性规划的解答题中建议使用直线平移法求出最优解,即将目标函数看成是一条直线,分析目标函数Z与直线截距的关系,进而求出最优解.
注意:最后要将所求最优解还原为实际问题.
(2)要求花费的最小值,即求可行域中的最优解,在线性规划的解答题中建议使用直线平移法求出最优解,即将目标函数看成是一条直线,分析目标函数Z与直线截距的关系,进而求出最优解.
注意:最后要将所求最优解还原为实际问题.
解答: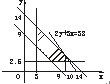 解:(1)依题意得v=
解:(1)依题意得v=
,w=
,4≤v≤20,30≤w≤100.
∴3≤x≤10,
≤y≤
.①
由于乘汽车、摩托艇所需的时间和x+y应在9至14个小时之间,即9≤x+y≤14.②
因此,满足①②的点(x,y)的存在范围是图中阴影部分(包括边界).
(2)∵p=100+3•(5-x)+2•(8-y),
∴3x+2y=131-p.
设131-p=k,那么当k最大时,p最小.
在通过图中的阴影部分区域(包括边界)且斜率为-
的直线3x+2y=k中,
使k值最大的直线必通过点(10,4),即当x=10,y=4时,p最小.
此时,v=12.5,w=30,p的最小值为93元.
 解:(1)依题意得v=
解:(1)依题意得v=| 50 |
| y |
| 300 |
| x |
∴3≤x≤10,
| 5 |
| 2 |
| 25 |
| 2 |
由于乘汽车、摩托艇所需的时间和x+y应在9至14个小时之间,即9≤x+y≤14.②
因此,满足①②的点(x,y)的存在范围是图中阴影部分(包括边界).
(2)∵p=100+3•(5-x)+2•(8-y),
∴3x+2y=131-p.
设131-p=k,那么当k最大时,p最小.
在通过图中的阴影部分区域(包括边界)且斜率为-
| 3 |
| 2 |
使k值最大的直线必通过点(10,4),即当x=10,y=4时,p最小.
此时,v=12.5,w=30,p的最小值为93元.
点评:在解决线性规划的应用题时,其步骤为:①分析题目中相关量的关系,列出不等式组,即约束条件?②由约束条件画出可行域?③分析目标函数Z与直线截距之间的关系?④使用平移直线法求出最优解?⑤还原到现实问题中.

练习册系列答案
相关题目
 某人上午7时,乘摩托艇以匀速v海里/时(4≤v≤20)从A港出发到距50海里的B港去,然后乘汽车以w千米/时(30≤w≤100)自B港向距300千米的C市驶去,应该在同一天下午4至9时到达C市.设汽车、摩托艇所需的时间分别是x,y小时.
某人上午7时,乘摩托艇以匀速v海里/时(4≤v≤20)从A港出发到距50海里的B港去,然后乘汽车以w千米/时(30≤w≤100)自B港向距300千米的C市驶去,应该在同一天下午4至9时到达C市.设汽车、摩托艇所需的时间分别是x,y小时.