题目内容
已知函数f(x)=2sinωxcosωx+cos2ωx-sin2ωx,(ω>0),若函数f(x)的最小正周期为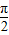 .
.(1)求ω的值,并求函数f(x)的最大值;
(2)若0<x<
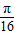 ,当f(x)=
,当f(x)=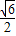 时,求
时,求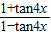 的值.
的值.
【答案】分析:(1)利用二倍角公式化简函数表达式,通过函数的周期公式,求ω的值,通过正弦函数的最大值求函数f(x)的最大值;
(2)利用0<x<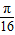 ,以及f(x)=
,以及f(x)=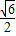 ,求出
,求出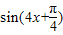 ,
,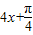 的值,然后求
的值,然后求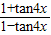 的值
的值
解答:解:(1)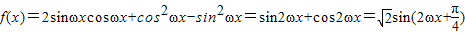 …(2分)
…(2分)
因为函数f(x)的最小正周期为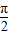 ,所以
,所以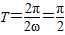 ,即ω=2…(3分)
,即ω=2…(3分)
此时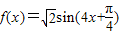 ,所以f(x)的最大值为
,所以f(x)的最大值为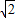 .…(5分)
.…(5分)
(2)当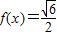 时,即
时,即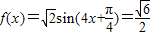 ,
,
化简得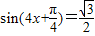 .…(7分)
.…(7分)
因为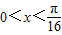 ,所以
,所以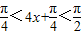 ,所以
,所以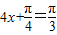 .…(9分)
.…(9分)
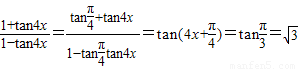 .…(12分)
.…(12分)
点评:本题是中档题,考查三角函数的化简求值,二倍角与两角和的正弦函数的应用,两角和的正切函数的应用,考查计算能力.
(2)利用0<x<
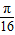 ,以及f(x)=
,以及f(x)=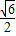 ,求出
,求出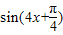 ,
,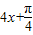 的值,然后求
的值,然后求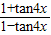 的值
的值解答:解:(1)
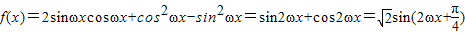 …(2分)
…(2分)因为函数f(x)的最小正周期为
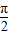 ,所以
,所以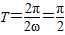 ,即ω=2…(3分)
,即ω=2…(3分)此时
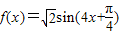 ,所以f(x)的最大值为
,所以f(x)的最大值为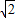 .…(5分)
.…(5分)(2)当
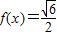 时,即
时,即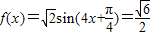 ,
,化简得
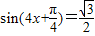 .…(7分)
.…(7分)因为
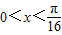 ,所以
,所以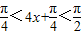 ,所以
,所以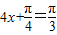 .…(9分)
.…(9分)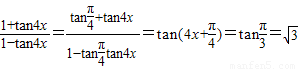 .…(12分)
.…(12分)点评:本题是中档题,考查三角函数的化简求值,二倍角与两角和的正弦函数的应用,两角和的正切函数的应用,考查计算能力.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目