题目内容
 (2009•青岛一模)在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=
(2009•青岛一模)在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为矩形,AB=PA=| 1 | a |
(Ⅰ)当a=1时,求证:BD⊥PC;
(Ⅱ)若BC边上有且只有一个点Q,使得PQ⊥QD,求此时二面角A-PD-Q的余弦值.
分析:(Ⅰ)由PA垂直矩形底面ABCD,利用直线与平面垂直的性质得到PA垂直BD,由a=1,知道底面ABCD为正方形,从而得到BD垂直于△PAC,由此能够证明BD⊥PC.
(Ⅱ)由AB,AD,AP两两垂直,分别以它们所在的直线为x轴,y轴,z轴,建立坐标系.借助空间向量先求出a=2,m=1.然后求出设面PQD的法向量
=(
,
,1),取面PAD的法向量
=(1,0,0),由此利用向量法能求出二面角A-PD-Q的余弦值.
(Ⅱ)由AB,AD,AP两两垂直,分别以它们所在的直线为x轴,y轴,z轴,建立坐标系.借助空间向量先求出a=2,m=1.然后求出设面PQD的法向量
| p |
| 1 |
| 2 |
| 1 |
| 2 |
| q |
解答:证明:(Ⅰ)∵PA垂直矩形底面ABCD,
∴PA垂直BD,
∵AB=PA=
BC(a>0),
a=1,
∴AB=PA=BC,
∴底面ABCD为正方形,
∴BD垂直于AC,
∴BD垂直于△PAC,
∴BD⊥PC.
解:(Ⅱ)∵AB,AD,AP两两垂直,分别以它们所在的直线为x轴,y轴,z轴,
建立坐标系
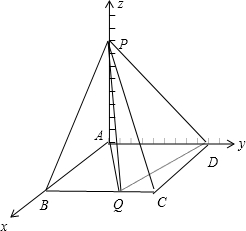
令AB=1,则BC=a,
B(1,0,0),D(0,a,0),C(1,a,0),P(0,0,1),
设BQ=m,Q(1,m,0),(0≤m≤a),
要使PQ⊥QD,只要
•
=-1+m(a-m)=0,
即m2-am+1=0,
由△=a2-4=0,得a=2,此时m=1.
∴BC边上有且只有一个点Q,使得PQ⊥QD时,
Q为BC的中点,且a=2,
设面PQD的法向量
=(x,y,1),
则
,即
,
∴
=(
,
,1),
取面PAD的法向量
=(1,0,0),
则<
,
>的大小与三面角A-PD-Q的大小相等,
∵cos<
,
>=
=
,
∴二面角A-PD-Q的余弦值为
.
∴PA垂直BD,
∵AB=PA=
| 1 |
| a |
a=1,
∴AB=PA=BC,
∴底面ABCD为正方形,
∴BD垂直于AC,
∴BD垂直于△PAC,
∴BD⊥PC.
解:(Ⅱ)∵AB,AD,AP两两垂直,分别以它们所在的直线为x轴,y轴,z轴,
建立坐标系

令AB=1,则BC=a,
B(1,0,0),D(0,a,0),C(1,a,0),P(0,0,1),
设BQ=m,Q(1,m,0),(0≤m≤a),
要使PQ⊥QD,只要
| PQ |
| QD |
即m2-am+1=0,
由△=a2-4=0,得a=2,此时m=1.
∴BC边上有且只有一个点Q,使得PQ⊥QD时,
Q为BC的中点,且a=2,
设面PQD的法向量
| p |
则
|
|
∴
| p |
| 1 |
| 2 |
| 1 |
| 2 |
取面PAD的法向量
| q |
则<
| p |
| q |
∵cos<
| p |
| q |
| ||||
|
|
| ||
| 6 |
∴二面角A-PD-Q的余弦值为
| ||
| 6 |
点评:本题以四棱锥为载体,考查线面平行,考查线面角,考查面面角,综合性强,难度大,容易出错.解决问题的关键是建立空间直角坐标系,利用向量法进行求解.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目