题目内容
某校选派4人参加上级组织的数学竞赛,现从甲、乙两个竞赛班各选派2人.设甲、乙两班选派的人员获奖概率分别为
和
,且4位选手是否获奖互不影响.
(I)求甲、乙两班各有1人获奖的概率;
(II)求该校获奖人数ξ的分布列与期望.
| 2 |
| 3 |
| 1 |
| 2 |
(I)求甲、乙两班各有1人获奖的概率;
(II)求该校获奖人数ξ的分布列与期望.
(I)设Ak表示甲班有k人获奖,K=0,1,2
Bi表示乙班有i人获奖,i=0,1,2.
P(Ak)=
(
)k(
)2-k;
P(Bi)=
(
)i(
)2-i;
据此算得P(A0)=
;P(A,1)=
;P(A2)=
P(B0)=
,P(B,1)=
,P(,B2)=
甲、乙两班各有1人获奖的概率为P(A1B1) =P(A1)P(B1) =
×
=
(II)ξ的所有可能值为0,1,2,3,4,且
P(ξ=0)=
×
=
P(ξ=1)=
×
+
×
=
P( A0 •B2)+P(A1B1)+P(A2B0)=
P(ξ=3)=
×
+
×
=
P(ξ=4)=
×
=
综上知ξ的分布列
从而,ξ的期望为Eξ=0×
+1×
+2×
+3×
+4×
=
Bi表示乙班有i人获奖,i=0,1,2.
P(Ak)=
| C | k2 |
| 2 |
| 3 |
| 1 |
| 3 |
P(Bi)=
| C | i2 |
| 1 |
| 2 |
| 1 |
| 2 |
据此算得P(A0)=
| 1 |
| 9 |
| 4 |
| 9 |
| 4 |
| 9 |
P(B0)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
甲、乙两班各有1人获奖的概率为P(A1B1) =P(A1)P(B1) =
| 4 |
| 9 |
| 1 |
| 2 |
| 2 |
| 9 |
(II)ξ的所有可能值为0,1,2,3,4,且
P(ξ=0)=
| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 36 |
P(ξ=1)=
| 1 |
| 9 |
| 1 |
| 2 |
| 4 |
| 9 |
| 1 |
| 4 |
| 1 |
| 6 |
P( A0 •B2)+P(A1B1)+P(A2B0)=
| 13 |
| 36 |
P(ξ=3)=
| 4 |
| 9 |
| 1 |
| 4 |
| 4 |
| 9 |
| 1 |
| 2 |
| 1 |
| 3 |
P(ξ=4)=
| 4 |
| 9 |
| 1 |
| 4 |
| 1 |
| 9 |
综上知ξ的分布列
| ξ | 0 | 1 | 2 | 3 | 4 |
| P | 1/36 | 1/6 | 13/36 | 1/3 | 1/9 |
| 1 |
| 36 |
| 1 |
| 6 |
| 13 |
| 36 |
| 1 |
| 3 |
| 1 |
| 9 |
| 7 |
| 3 |

练习册系列答案
相关题目
 和
和 ,且4位选手是否获奖互不影响.
,且4位选手是否获奖互不影响.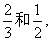 且4位选手是否获奖互不影响.
且4位选手是否获奖互不影响. 的分布列与期望.
的分布列与期望.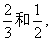 且4位选手是否获奖互不影响.
且4位选手是否获奖互不影响. 的分布列与期望.
的分布列与期望.