题目内容
7.过椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1的左焦点F引直线交椭圆于A、B两点,若|AB|=7,则此直线的方程为$\sqrt{3}x$+2y+2$\sqrt{3}$=0或$\sqrt{3}x$-2y+2$\sqrt{3}$=0.分析 先由椭圆方程求出右焦点F的坐标,然后利用待定系数法给出AB的方程,与椭圆的方程联立,消去y,得到关于x的一元二次方程,最后利用韦达定理、弦长公式求出直线的斜率,注意单独验证斜率不存在的情况.
解答 解:椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1得a2=16,b2=12,
∴c=$\sqrt{{a}^{2}-{b}^{2}}$=2,∴F(-2,0),
对于直线AB,
当AB⊥x轴时,将x=-2代入椭圆方程得y=±3,
∴|AB|=6,∴AB不垂直于x轴,
设直线AB方程为y=k(x+2),代入椭圆方程整理得
(3+4k2)x2+16k2x+16k2-48=0,
设A(x1,y1),B(x2,y2),
∴x1+x2=$\frac{-16{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{16{k}^{2}-48}{3+4{k}^{2}}$,
∴|AB|=$\sqrt{(1+{k}^{2})[(\frac{-16{k}^{2}}{3+4{k}^{2}})^{2}-\frac{64{k}^{2}-192}{3+4{k}^{2}}]}$=$\frac{24(1+{k}^{2})}{3+4{k}^{2}}$=7,
化简后得k2=$\frac{3}{4}$,∴k=±$\frac{\sqrt{3}}{2}$,
∴AB的方程为$\sqrt{3}x$+2y+2$\sqrt{3}$=0或$\sqrt{3}x$-2y+2$\sqrt{3}$=0.
故答案为:$\sqrt{3}x$+2y+2$\sqrt{3}$=0或$\sqrt{3}x$-2y+2$\sqrt{3}$=0.
点评 本题重点考查了椭圆的标准方程及其性质以及直线与椭圆的位置关系,一般是将直线方程代入椭圆方程消去y(或x)的一元二次方程,然后进一步求解;本题是借助韦达定理、弦长公式构造出关于k的方程求解,计算量较大,需在计算时认真、细心.

| A. | 2 | B. | 4 | C. | $\frac{8\sqrt{3}}{3}$ | D. | $\frac{16\sqrt{3}}{3}$ |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
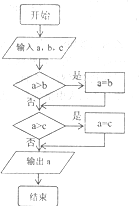
| A. | 求a、b、c三数的最大数 | B. | 求a、b、c三数的最小数 | ||
| C. | 将a、b、c三数由大到小排列 | D. | 将a、b、c三数由小到大排列 |
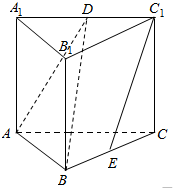 直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.
直三棱柱ABC-A1B1C1中,AA1=AC,AB⊥AC,D,E分别是A1C1,BC的中点.