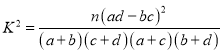题目内容
【题目】一款小游戏的规则如下:每轮游戏要进行三次,每次游戏都需要从装有大小相同的2个红球,3个白球的袋中随机摸出2个球,若摸出的“两个都是红球”出现3次获得200分,若摸出“两个都是红球”出现1次或2次获得20分,若摸出“两个都是红球”出现0次则扣除10分(即获得![]() 分).
分).
(1)设每轮游戏中出现“摸出两个都是红球”的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)玩过这款游戏的许多人发现,若干轮游戏后,与最初的分数相比,分数没有增加反而减少了,请运用概率统计的相关知识分析解释上述现象.
【答案】(1)分布列见解析;(2)见解析
【解析】
(1)求出每次游戏,出现“两个都是红球”的概率为![]() ,再根据二项分布可求得
,再根据二项分布可求得![]() 的分布列;
的分布列;
(2)设每轮游戏得分为![]() ,进而求出
,进而求出![]() 的期望值为负数,即可得到结论.
的期望值为负数,即可得到结论.
(1)每次游戏,出现“两个都是红球”的概率为![]() .
.
![]() 可能的取值为0,1,2,3,
可能的取值为0,1,2,3,
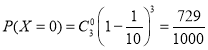 ,
,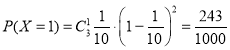 ,
,
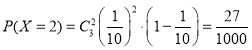 ,
,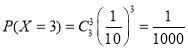 ,
,
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
(2)设每轮游戏得分为![]() .
.
由(1)知,![]() 的分布列为:
的分布列为:
|
| 20 | 200 |
|
|
|
|
![]() 的数学期望为
的数学期望为![]() .
.
这表明,获得分数![]() 的期望为负.因此,多次游戏之后大多数人的分数减少了.
的期望为负.因此,多次游戏之后大多数人的分数减少了.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案【题目】上世纪末河南出土的以鹤的尺骨(翅骨)制成的“骨笛”(图1),充分展示了我国古代高超的音律艺术及先进的数学水平,也印证了我国古代音律与历法的密切联系.图2为骨笛测量“春(秋)分”,“夏(冬)至”的示意图,图3是某骨笛的部分测量数据(骨笛的弯曲忽略不计),夏至(或冬至)日光(当日正午太阳光线)与春秋分日光(当日正午太阳光线)的夹角等于黄赤交角.

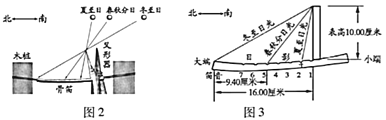
由历法理论知,黄赤交角近1万年持续减小,其正切值及对应的年代如下表:
黄赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根据以上信息,通过计算黄赤交角,可估计该骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
【题目】某工厂计划建设至少3个,至多5个相同的生产线车间,以解决本地区公民对特供商品![]() 的未来需求.经过对先期样本的科学性调查显示,本地区每个月对商品
的未来需求.经过对先期样本的科学性调查显示,本地区每个月对商品![]() 的月需求量均在50万件及以上,其中需求量在50~ 100万件的频率为0.5,需求量在100~200万件的频率为0.3,不低于200万件的频率为0.2.用调查样本来估计总体,频率作为相应段的概率,并假设本地区在各个月对本特供商品
的月需求量均在50万件及以上,其中需求量在50~ 100万件的频率为0.5,需求量在100~200万件的频率为0.3,不低于200万件的频率为0.2.用调查样本来估计总体,频率作为相应段的概率,并假设本地区在各个月对本特供商品![]() 的需求相互独立.
的需求相互独立.
(1)求在未来某连续4个月中,本地区至少有2个月对商品![]() 的月需求量低于100万件的概率.
的月需求量低于100万件的概率.
(2)该工厂希望尽可能在生产线车间建成后,车间能正常生产运行,但每月最多可正常生产的车间数受商品![]() 的需求量
的需求量![]() 的限制,并有如下关系:
的限制,并有如下关系:
商品 |
|
|
|
车间最多正常运行个数 | 3 | 4 | 5 |
若一个车间正常运行,则该车间月净利润为1500万元,而一个车间未正常生产,则该车间生产线的月维护费(单位:万元)与月需求量有如下关系:
商品 |
|
|
未正常生产的一个车间的月维护费(万元) | 500 | 600 |
试分析并回答该工厂应建设生产线车间多少个?使得商品![]() 的月利润为最大.
的月利润为最大.