题目内容
已知函数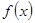 满足
满足 且
且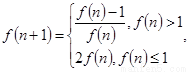 若对于任意的
若对于任意的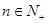 总有
总有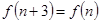 成立,则
成立,则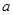 在
在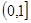 内的可能值有( )个
内的可能值有( )个
A.1 B.2 C.3 D.4
【答案】
B
【解析】
试题分析::∵0<a≤1,∴f(2)=2f(1)=2a,
① 当0<a≤1/4时,0<2a≤1/2,0<4a≤1,
∴f(3)=2f(2)=4a,
f(4)=2f(3)=8a,
此时f(4)=f(1)不成立;
② 当1/4<a≤1/2时,1/2<2a≤1,1<4a≤2,
∴f(3)=2f(2)=4a,
f(4)=[f(3)-1]/f(3)=﹙4a-1﹚/4a,
此时f(4)=f(1)?﹙4a-1﹚/4a=a?a=1/2;
③ 当1/2<a≤1时,1<2a≤2,2<4a≤4,
∴f(3)=[f(2)-1]/f(2)=(2a-1)/2a≤1/2,
∴f(4)=2f(3)=(2a-1)/a,
此时f(4)=f(1)?(2a-1)/a=a?a=1;
综上所述,当n=1时,有f(n+3)=f(n)成立时,
则a在(0,1]内的可能值有两个.故选B。
考点:分段函数、函数等式恒成立问题。
点评:中档题,本题综合考查分段函数的概念、函数等式恒成立问题、方程式的解法等基础知识,考查运算求解能力,考查分类讨论思想、化归与转化思想.是一道不错的题目。

练习册系列答案
相关题目
 满足对任意实数
满足对任意实数 都有
都有 成立,且当
成立,且当 时,
时, ,
, .
. 的值;
的值; 上的单调性,并证明;
上的单调性,并证明; ,总能找到一个正实数
,总能找到一个正实数 ,使得当
,使得当 时,
时, ,则称函数
,则称函数 处连续。试证明:
处连续。试证明: 处连续.
处连续. 满足:对于任意实数
满足:对于任意实数 ,都有
,都有 恒成立,且当
恒成立,且当 时,
时, 恒成立;
恒成立; 的值,并例举满足题设条件的一个特殊的具体函数;
的值,并例举满足题设条件的一个特殊的具体函数; 在R上的单调性,并加以证明;
在R上的单调性,并加以证明;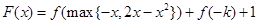 (其中
(其中 )有三个零点
)有三个零点 ,求
,求 的取值范围.
的取值范围.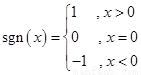 ,若已知函数
,若已知函数 (
(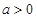 且
且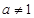 )满足
)满足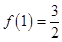 .
. ;
; 对于任意正实数
对于任意正实数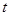 恒成立,求实数
恒成立,求实数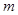 的取值范围.
的取值范围. ,若已知函数
,若已知函数