题目内容
(本小题满分12分)
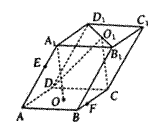如图，已知平行六面体ABCD—A1B1C1D1的底面为矩形，O1，O分别为上、下底面的中心，且A1在底面ABCD的射影是O，AB = 8，BC = AA1 = 6．
求证：平面O1DC⊥平面ABCD；
若点E、F分别在棱AA1、BC上，且AE = 2EA1，问点F在何处时EF⊥AD；
在 (2) 的条件下，求F到平面CC1O1距离．
(1) 证明：∵ A1O1
OC
∴ A1OCO1为平行四边形
∴ A1O∥O1C 2分
∵ A1O⊥平面ABCD
∴ O1C⊥平面ABCD 3分
∴平面O1DC⊥平面ABCD 4分
(2) 解：在AO上取点G，使AG = 2GO，则EG∥A1O
∴ EG⊥平面ABCD
∴ 当且仅当FG⊥AD时，EF⊥AD
∴ FG∥AB
∵ CG = 2AG
∴ CF = 2BF
即当CF = 2FB时，结论成立． 7分
(3) 解：作FH⊥AC
∵ CO1⊥平面ABCD
∴ 平面C1O1C⊥平面ABCD
∴ FH⊥面C1O1C
∵ △FCH∽△ACB
∴ 
而AC = 10，CF = 4 ∴ 
∴ F到平面CC1O1的距离为
12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
