题目内容
一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.(1)建立如图所示的平面直角坐标系xoy,试求拱桥所在抛物线的方程;
(2)若一竹排上有一4米宽6米高的大木箱,问此木排能否安全通过此桥?
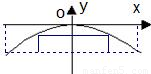
【答案】分析:(1)设抛物线方程x2=-2py,抛物线过点(26,-6.5),代入抛物线方程求出参数p 即得抛物线方程.
(2)把x=2代入抛物线的方程求得y值,由6.5-6=0.5>求得的y值,可知木排能安全通过此桥.
解答:解:(1)设抛物线方程x2=-2py.(2分)
由题意可知,抛物线过点(26,-6.5),代入抛物线方程,得
262=13p,解得p=52,所以,抛物线方程为 x2 =-104y.(6分)
(2)把x=2代入,求得y=-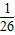 .(9分)
.(9分)
而6.5-6=0.5>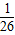 ,所以木排能安全通过此桥.(12分)
,所以木排能安全通过此桥.(12分)
点评:本题考查用待定系数法求抛物线的标准方程的方法,以及利用抛物线的方程解决实际问题.
(2)把x=2代入抛物线的方程求得y值,由6.5-6=0.5>求得的y值,可知木排能安全通过此桥.
解答:解:(1)设抛物线方程x2=-2py.(2分)
由题意可知,抛物线过点(26,-6.5),代入抛物线方程,得
262=13p,解得p=52,所以,抛物线方程为 x2 =-104y.(6分)
(2)把x=2代入,求得y=-
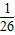 .(9分)
.(9分)而6.5-6=0.5>
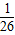 ,所以木排能安全通过此桥.(12分)
,所以木排能安全通过此桥.(12分)点评:本题考查用待定系数法求抛物线的标准方程的方法,以及利用抛物线的方程解决实际问题.

练习册系列答案
相关题目
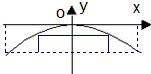 一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.
一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.(1)建立如图所示的平面直角坐标系xoy,试求拱桥所在抛物线的方程;
(2)若一竹排上有一4米宽6米高的大木箱,问此木排能否安全通过此桥?
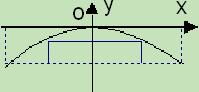

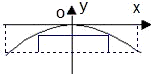 一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.
一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.