题目内容
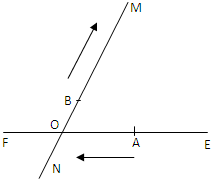如图，有两条相交成| π |
| 3 |
| e1 |
| e2 |
（1）求
| e1 |
| e2 |
（2）若过2小时后，甲到达C点，乙到达D点，请用
| e1 |
| e2 |
| CD |
（3）若过t小时后，甲到达G点，乙到达H点，请用
| e1 |
| e2 |
| GH |
（4）什么时间两人间距最短？
分析：（1）由题意结合向量的数乘的意义可得答案；
（2）若过2小时后，易得CD的位置，用
，和
，可表示向量
和
，而
=
-
，代入可得；
（3）同（2的方法）可得；
（4）两人间距离y=|
|，代入化简可得y=
，由二次函数的知识可得答案．
（2）若过2小时后，易得CD的位置，用
| e1 |
| e2 |
| OC |
| OD |
| CD |
| OD |
| OC |
（3）同（2的方法）可得；
（4）两人间距离y=|
| GH |
| 12t2-6t+3 |
解答：解：（1）由题意可得
=
，
=
，
（2）若过2小时后，甲到达C点，乙到达D点，
则
=-2
，
=5
，
故
=
-
=2
+5
，
（3）同（2）可得：经过t小时后，甲到达G点，乙到达H点，
则
=（-2t+2）
，
=（2t+1）
，
故
=
-
=（2t-2）
+（2t+1）
，
（4）由（3）可得
=（2t-2）
+（2t+1）
，
故两人间距离y=|
|=
=
=
，
由二次函数的知识可知，当t=-
=
时，
上式取到最小值
，故
时两人间距离最短．
| e1 |
| 1 |
| 2 |
| OA |
| e2 |
| OB |
（2）若过2小时后，甲到达C点，乙到达D点，
则
| OC |
| e1 |
| OD |
| e2 |
故
| CD |
| OD |
| OC |
| e1 |
| e2 |
（3）同（2）可得：经过t小时后，甲到达G点，乙到达H点，
则
| OG |
| e1 |
| OH |
| e2 |
故
| GH |
| OH |
| OG |
| e1 |
| e2 |
（4）由（3）可得
| GH |
| e1 |
| e2 |
故两人间距离y=|
| GH |
[(2t-2)
|
=
(2t-2)2+(2t+1)2+2(2t-2)(2t+1)×
|
=
| 12t2-6t+3 |
由二次函数的知识可知，当t=-
| -6 |
| 2×12 |
| 1 |
| 4 |
上式取到最小值
| 3 |
| 2 |
| 1 |
| 4 |
点评：本题考查向量的平行以及单位向量和模长的求解，属中档题．
练习册系列答案
相关题目
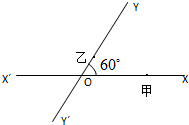如图，有两条相交成60°的直路XX′，YY′，交点是O，甲、乙分别在OX，OY上，起初甲离O点3km，乙离O点1km，后甲沿XX′方向用2km/h的速度，乙沿Y′Y方向用4km/h的速度同时步行．设t小时后甲在XX′上点A处，乙在YY′上点B处．
角的直路
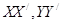,交点为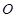
,甲、乙分别在
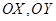上，起初甲离
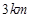，乙离
，后来甲沿
的方向，乙沿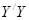
的方向，同时以
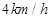的速度步行。
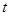小时后两人的距离是多少？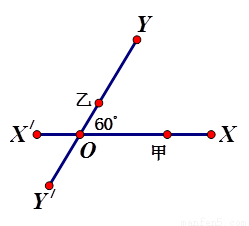
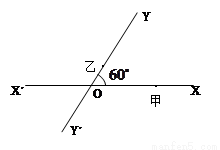
的直路
，
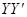，交点是
，甲、乙分别在
上，起初甲离O点3 km，乙离O点1 km，后甲沿
方向用4km/h的速度同时步行. 设t小时后甲在