题目内容
已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数,e=2.718…,且函数y=f(x)和y=g(x)的图像在它们与坐标轴交点处的切线互相平行.
(1)求常数a的值;(2)若存在x使不等式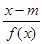 >
> 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)对于函数y=f(x)和y=g(x)公共定义域内的任意实数x0,我们把|f(x0)-g(x0)|的值称为两函数在x0处的偏差.求证:函数y=f(x)和y=g(x)在其公共定义域内的所有偏差都大于2.
(1) a=1.(2) (-∞,0).(3)详见解析.
解析试题分析:(1)求出交点,切线平行即导数值相等可解;(2)转化为新函数,求出导数,利用单调性极值解;(3)构造新函数求导,利用单调性证明.
试题解析:(1)f(x)与坐标轴的交点为(0,a),f′(0)=a,g(x)与坐标轴的交点为(a,0),g′(a)=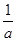 .
.
∴a=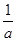 ,得a=±1,又a>0,故a=1.
,得a=±1,又a>0,故a=1.
(2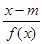 >
> 可化为m<x-
可化为m<x- ex.令h(x)=x-
ex.令h(x)=x- ex,则h′(x)=1-(
ex,则h′(x)=1-(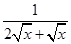 )ex.
)ex.
∵x>0,∴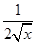 +
+ ≥
≥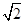 ,ex>1
,ex>1
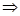 (
(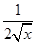 +
+ )ex>1.故h′(x)<0.
)ex>1.故h′(x)<0.
∴h(x)在(0,+∞)上是减函数,因此h(x)<h(0)=0. ∴实数m的取值范围是(-∞,0).
(3)y=f(x)与y=g(x)的公共定义域为(0,+∞),|f(x)-g(x)|=|ex-lnx|=ex-lnx.
令h(x)=ex-x-1,则h′(x)=ex-1>0.∴h(x)在(0,+∞)上是增函数.
故h(x)>h(0)=0,即ex-1>x. ①
令m(x)=lnx-x+1,则m′(x)=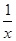 -1.
-1.
当x>1时,m′(x)<0,当0<x<1时,m′(x)>0.∴m(x)有最大值m(1)=0,因此lnx+1<x. ②
由①②,得ex-1>lnx+1,即ex-lnx>2.
∴函数y=f(x)和y=g(x)在其公共定义域内的所有偏差都大于2.
考点:导数几何意义、极值、导数的应用.

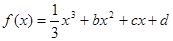 ,设曲线
,设曲线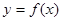 在与
在与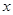 轴交点处的切线为
轴交点处的切线为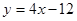 ,
,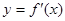 为
为 的导函数,满足
的导函数,满足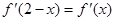 .
.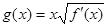 ,
,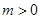 ,求函数
,求函数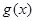 在
在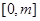 上的最大值;
上的最大值;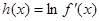 ,若对于一切
,若对于一切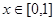 ,不等式
,不等式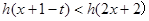 恒成立,求实数
恒成立,求实数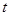 的取值范围.
的取值范围.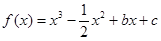 。
。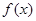 在
在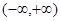 是增函数,求b的取值范围;
是增函数,求b的取值范围;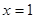 时取得极值,且
时取得极值,且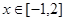 时,
时,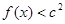 恒成立,求c的取值范围.
恒成立,求c的取值范围. 为实数,函数
为实数,函数
 的单调区间与极值;
的单调区间与极值; 且
且 时,
时,
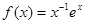 的定义域为(0,
的定义域为(0,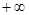 ).
).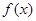 在
在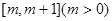 上的最小值;
上的最小值; ,如果
,如果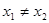 ,且
,且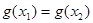 ,证明:
,证明: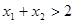 .
.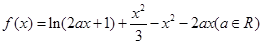
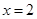 为
为 的极值点,求实数
的极值点,求实数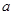 的值;
的值; 在
在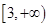 上为增函数,求实数
上为增函数,求实数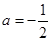 时,方程
时,方程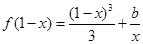 有实根,求实数
有实根,求实数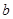 的最大值.
的最大值.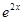 +2x+m,x∈R
+2x+m,x∈R +2mx+1.
+2mx+1. .
. 的最小正周期
的最小正周期 ;
;
 ,
, ,
, ,以及
,以及 围成的平面图形的面积.
围成的平面图形的面积. :
: 上一点
上一点 作曲线
作曲线 交
交 轴于点
轴于点 ,又过
,又过 作
作  ,然后再过
,然后再过 交
交 ,又过
,又过 作
作 ,
, ,以此类推,过点
,以此类推,过点 的切线
的切线 与
与 ,再过点
,再过点 作
作 (
( N
N ).
). 、
、 及数列
及数列 的通项公式;(2) 设曲线
的通项公式;(2) 设曲线 所围成的图形面积为
所围成的图形面积为 ,求
,求 的前
的前 项和为
项和为 ,求证:
,求证:
 N
N .
.