题目内容
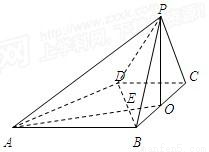
已知平面PAD⊥平面ABCD,PA=PD=2,矩形ABCD的边长AB=DC=2,AD=BC= .
.(Ⅰ)证明:直线AD∥平面PBC;
(Ⅱ)求直线PC和底面ABCD所成角的大小.

【答案】分析:(I)矩形ABCD中,根据AD∥BC,结合直线与平面平行的判定定理,可得直线AD∥平面PBC;
(II)由面面垂直的判定定理,证出PE⊥平面ABCD且CD⊥平面PAD,可得∠PCE就是直线PC和底面ABCD所成的角,且CD⊥PD.在Rt△PCE中,算出PE、PC的长,从而得到sin∠PCE= ,得∠PCE=30°,得到直线PC和底面ABCD所成角的大小.
,得∠PCE=30°,得到直线PC和底面ABCD所成角的大小.
解答: 解:(Ⅰ)∵四边形ABCD是矩形,∴AD∥BC,…(2分)
解:(Ⅰ)∵四边形ABCD是矩形,∴AD∥BC,…(2分)
又∵BC⊆平面PBC,AD?平面PBC
∴直线直线AD∥平面PBC;…(5分)
(Ⅱ)过点P作PE⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PE⊥平面ABCD,同理可得CD⊥平面PAD;…(8分)
所以,直线EC是直线PC在平面ABCD内的射影
∠PCE就是直线PC和底面ABCD所成的角,
∵CD⊥平面PAD且PD⊆平面PAD,∴CD⊥PD…(10分)
在Rt△PCD中,PC=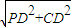 =2
=2
∵PA=PD=2,∴PE=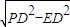 =
=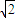
在Rt△PCE中,sin∠PCE=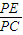 =
= ,可得∠PCE=30°…(11分)
,可得∠PCE=30°…(11分)
直线PC和底面ABCD所成角的大小为30°.…(12分)
点评:本题给出底面为矩形且一个侧面与底面垂直的四棱锥,证明线面平面并求直线与平面所成角的大小,着重考查了线面平行的判定、面面垂直的判定与性质和直线与平面所成角大小的求法等知识,属于中档题.
(II)由面面垂直的判定定理,证出PE⊥平面ABCD且CD⊥平面PAD,可得∠PCE就是直线PC和底面ABCD所成的角,且CD⊥PD.在Rt△PCE中,算出PE、PC的长,从而得到sin∠PCE=
 ,得∠PCE=30°,得到直线PC和底面ABCD所成角的大小.
,得∠PCE=30°,得到直线PC和底面ABCD所成角的大小.解答:
 解:(Ⅰ)∵四边形ABCD是矩形,∴AD∥BC,…(2分)
解:(Ⅰ)∵四边形ABCD是矩形,∴AD∥BC,…(2分)又∵BC⊆平面PBC,AD?平面PBC
∴直线直线AD∥平面PBC;…(5分)
(Ⅱ)过点P作PE⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PE⊥平面ABCD,同理可得CD⊥平面PAD;…(8分)
所以,直线EC是直线PC在平面ABCD内的射影
∠PCE就是直线PC和底面ABCD所成的角,
∵CD⊥平面PAD且PD⊆平面PAD,∴CD⊥PD…(10分)
在Rt△PCD中,PC=
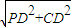 =2
=2
∵PA=PD=2,∴PE=
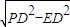 =
=
在Rt△PCE中,sin∠PCE=
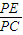 =
= ,可得∠PCE=30°…(11分)
,可得∠PCE=30°…(11分)直线PC和底面ABCD所成角的大小为30°.…(12分)
点评:本题给出底面为矩形且一个侧面与底面垂直的四棱锥,证明线面平面并求直线与平面所成角的大小,着重考查了线面平行的判定、面面垂直的判定与性质和直线与平面所成角大小的求法等知识,属于中档题.

练习册系列答案
相关题目
 (2012•武昌区模拟)已知平面PAD⊥平面ABCD,PA=PD=2,矩形ABCD的边长AB=DC=2,AD=BC=
(2012•武昌区模拟)已知平面PAD⊥平面ABCD,PA=PD=2,矩形ABCD的边长AB=DC=2,AD=BC=