题目内容
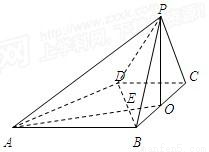
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=BCD=90°,AB=BC=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC中点,AO交BD于E.(1)求证:PA⊥BD;
(2)求二面角P-DC-B的大小;
(3)求证:平面PAD⊥平面PAB.
【答案】分析:(1)PO⊥BC⇒PO⊥平面ABCD,又AO⊥BD⇒PA⊥BD
(2)DC⊥PC,∠BCD=90°,∴∠PCB为二面角P-DC-B的平面角
(3)取PB的中点N⇒CN⊥PB,又平面PBC⊥平面PAB,AB⊥平面PBC⇒CN⊥AB⇒CN⊥平面PAB,又MNCD为平行四边形⇒DM⊥平面PAB⇒平面PAD⊥平面PAB.
解答: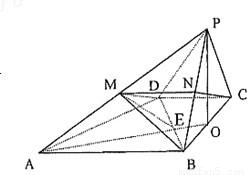 方法一:(1)证明:∵PB=PC,∴PO⊥BC
方法一:(1)证明:∵PB=PC,∴PO⊥BC
又∵平面PBC⊥平面ABCD
平面PBC∩平面ABCD=BC,∴PO⊥平面ABCD(2分)
在梯形ABCD中,可得Rt△ABO≌Rt△BCD∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,
即AO⊥BD∵PA在平面ABCD内的射影为AO,∴PA⊥BD(4分)
(2)解:∵DC⊥BC,且平面PBC⊥平面ABCD
∴DC⊥平面PBC∵PC?平面PBC,∴DC⊥PC
∴∠PCB为二面角P-DC-B的平面角(6分)
∵△PBC是等边三角形,∴∠PCB=60°,即二面角P-DC-B的大小为60°(8分)
(3)证明:取PA,PB的中点M,N,连接CN
∵PC=BC,∴CN⊥PB①∵AB⊥BC,且平面PBC⊥平面ABCD∴AB⊥平面PBC(10分)
∵AB?平面PAB∴平面PBC⊥平面PAB,CN⊥AB②
由①、②知CN⊥平面PAB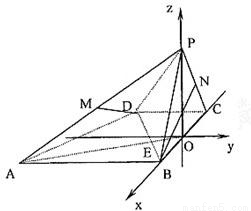
连接DM、MN,则由MN∥AB∥CD
MN= AB=CD,得四边形MNCD为平行四边形
AB=CD,得四边形MNCD为平行四边形
∴CN∥DM
∴DM⊥平面PAB
∵DM⊆平面PAD∴平面PAD⊥平面PAB(12分)
方法二:取BC的中点O,因为△PBC是等边三角形,
由侧面PBC⊥底面ABCD得PO⊥底面ABCD(1分)
以BC中点O为原点,以BC所在直线为x轴,过点O与
AB平行的直线为y轴,建立如图所示的空间直角坐标系
O-xyz(2分)
(1)证明:∵CD=1,则在直角梯形中,AB=BC=2
在等边三角形PBC中,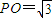
∴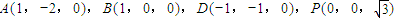
∴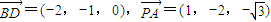
∵
∴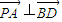 ,即PA⊥BD(4分)
,即PA⊥BD(4分)
(2)解:取PC中点N,则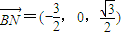
∵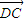 =(0,2,0),
=(0,2,0),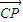 =(1,0,
=(1,0,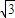 )
)
∴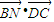 =(-
=(- )×0+0×2+
)×0+0×2+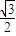 ×0=0
×0=0
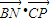 =(-
=(- )×1+0×0+
)×1+0×0+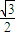 ×
×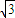 =0
=0
∴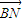 ⊥平面PDC,显然
⊥平面PDC,显然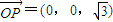 ,且
,且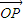 ⊥平面ABCD
⊥平面ABCD
∴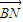 、
、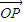 所夹角等于所求二面角的平面角(6分)∵
所夹角等于所求二面角的平面角(6分)∵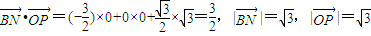
∴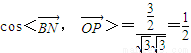 ∴二面角P-DC-B的大小为60°(8分)
∴二面角P-DC-B的大小为60°(8分)
(3)证明:取PA的中点M,连接DM,则M的坐标为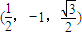
又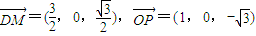 (10分)
(10分)
∴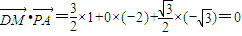
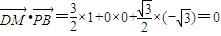
∴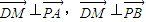 ,即DM⊥PA,DM⊥PB
,即DM⊥PA,DM⊥PB
∴DM⊥平面PAB,∴平面PAD⊥平面PAB.
点评:证明面面垂直的方法有两种,一是利用面面垂直的定义,既证两平面所成的二面角为直二面角,二是利用面面垂直的判定定理,既证一个平面过另一个平面的一条垂线.
(2)DC⊥PC,∠BCD=90°,∴∠PCB为二面角P-DC-B的平面角
(3)取PB的中点N⇒CN⊥PB,又平面PBC⊥平面PAB,AB⊥平面PBC⇒CN⊥AB⇒CN⊥平面PAB,又MNCD为平行四边形⇒DM⊥平面PAB⇒平面PAD⊥平面PAB.
解答:
 方法一:(1)证明:∵PB=PC,∴PO⊥BC
方法一:(1)证明:∵PB=PC,∴PO⊥BC又∵平面PBC⊥平面ABCD
平面PBC∩平面ABCD=BC,∴PO⊥平面ABCD(2分)
在梯形ABCD中,可得Rt△ABO≌Rt△BCD∴∠BEO=∠OAB+∠DBA=∠DBC+∠DBA=90°,
即AO⊥BD∵PA在平面ABCD内的射影为AO,∴PA⊥BD(4分)
(2)解:∵DC⊥BC,且平面PBC⊥平面ABCD
∴DC⊥平面PBC∵PC?平面PBC,∴DC⊥PC
∴∠PCB为二面角P-DC-B的平面角(6分)
∵△PBC是等边三角形,∴∠PCB=60°,即二面角P-DC-B的大小为60°(8分)
(3)证明:取PA,PB的中点M,N,连接CN
∵PC=BC,∴CN⊥PB①∵AB⊥BC,且平面PBC⊥平面ABCD∴AB⊥平面PBC(10分)
∵AB?平面PAB∴平面PBC⊥平面PAB,CN⊥AB②
由①、②知CN⊥平面PAB

连接DM、MN,则由MN∥AB∥CD
MN=
 AB=CD,得四边形MNCD为平行四边形
AB=CD,得四边形MNCD为平行四边形∴CN∥DM
∴DM⊥平面PAB
∵DM⊆平面PAD∴平面PAD⊥平面PAB(12分)
方法二:取BC的中点O,因为△PBC是等边三角形,
由侧面PBC⊥底面ABCD得PO⊥底面ABCD(1分)
以BC中点O为原点,以BC所在直线为x轴,过点O与
AB平行的直线为y轴,建立如图所示的空间直角坐标系
O-xyz(2分)
(1)证明:∵CD=1,则在直角梯形中,AB=BC=2
在等边三角形PBC中,
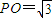
∴
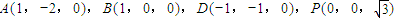
∴
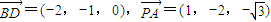
∵

∴
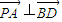 ,即PA⊥BD(4分)
,即PA⊥BD(4分)(2)解:取PC中点N,则
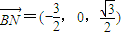
∵
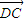 =(0,2,0),
=(0,2,0),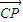 =(1,0,
=(1,0,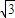 )
)∴
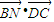 =(-
=(- )×0+0×2+
)×0+0×2+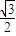 ×0=0
×0=0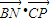 =(-
=(- )×1+0×0+
)×1+0×0+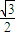 ×
×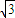 =0
=0∴
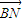 ⊥平面PDC,显然
⊥平面PDC,显然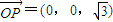 ,且
,且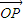 ⊥平面ABCD
⊥平面ABCD∴
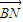 、
、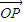 所夹角等于所求二面角的平面角(6分)∵
所夹角等于所求二面角的平面角(6分)∵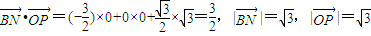
∴
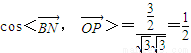 ∴二面角P-DC-B的大小为60°(8分)
∴二面角P-DC-B的大小为60°(8分)(3)证明:取PA的中点M,连接DM,则M的坐标为
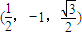
又
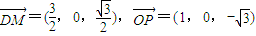 (10分)
(10分)∴
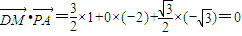
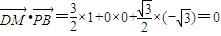
∴
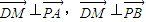 ,即DM⊥PA,DM⊥PB
,即DM⊥PA,DM⊥PB∴DM⊥平面PAB,∴平面PAD⊥平面PAB.
点评:证明面面垂直的方法有两种,一是利用面面垂直的定义,既证两平面所成的二面角为直二面角,二是利用面面垂直的判定定理,既证一个平面过另一个平面的一条垂线.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,