题目内容
在(ax+1)7的展开式中,x3项的系数是x2的系数与x5项系数的等比中项,则a的值是( )A.

B.

C.

D.
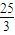
【答案】分析:先写成展开式的通项,进而可得项的系数,利用x3项的系数是x2的系数与x5项系数的等比中项,可建立方程,从而求出a的值.
解答:解:展开式的通项为:Tr+1=C7r(ax)7-r
∴x3项的系数是C74a3,x2项的系数是C75a2,x5项的系数是C72a5
∵x3项的系数是x2的系数与x5项系数的等比中项
∴(C74a3)2=C75a2×C72a5
∴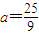
故选B.
点评:本题以二项式为载体,考查展开式的通项公式,考查等比中项,解题的关键是正确写出二项展开式的通项.
解答:解:展开式的通项为:Tr+1=C7r(ax)7-r
∴x3项的系数是C74a3,x2项的系数是C75a2,x5项的系数是C72a5
∵x3项的系数是x2的系数与x5项系数的等比中项
∴(C74a3)2=C75a2×C72a5
∴
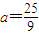
故选B.
点评:本题以二项式为载体,考查展开式的通项公式,考查等比中项,解题的关键是正确写出二项展开式的通项.

练习册系列答案
相关题目



