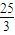Question

（ax+1）⁷的展开式中，x³的系数是x²的系数与x⁴的系数的等差中项．若实数a＞1，那么a=

 

．

Answer 1

分析：先写出二项展开式的通项公式，利用通项公式分别写出x³、x²、x⁴的系数，再用等差中项的概念列出方程，解方程即可．

解答：解：T_k+1=C₇^K（ax）^7-k=C₇^ka^7-kx^7-k，
故x³、x²、x⁴的系数分别为C₇⁴a³，C₇⁵a²和C₇³a⁴，
由题意2C₇⁴a³=C₇⁵a²+C₇³a⁴
解得：a=1+

10

5

故答案为：1+

10

5

点评：本题考查二项式定理的通项公式的应用、二项式系数问题、等差中项的概念及组合数的运算等知识，属基本题型的考查．