题目内容
已知定义在实数集R上的奇函数f（x），当x＞0时，f（x）的图象是抛物线的一部分，且该抛物线经过点（1，0）、（3，0）和（0，3）．（1）求出f（x）的解析式；
（2）写出f（x）的单调区间；
（3）已知集合A={（x，y）|y=f（x）}，B={（x，y）|y=t，x∈R，t∈R}，若A∩B有4个元素，求实数t的取值范围．
分析：（1）利用二次函数的零点式，结合图中三个已知点的坐标求出：当x＞0时，f（x）=x2-4x+3．再根据函数为奇函数，解出x＜0和x=0时的表达式，即可得到f（x）的解析式；
（2）由函数单调区间的定义，结合函数的图象即可写出f（x）的单调区间；
（3）作出直线y=t并进行平移，观察它与函数y=f（x）的图象公共点的个数，并结合计算函数的极值即可得出满足条件的实数t的取值范围．
（2）由函数单调区间的定义，结合函数的图象即可写出f（x）的单调区间；
（3）作出直线y=t并进行平移，观察它与函数y=f（x）的图象公共点的个数，并结合计算函数的极值即可得出满足条件的实数t的取值范围．
解答：解：（1）根据题意，可得
∵当x＞0时，抛物线经过点（1，0）、（3，0），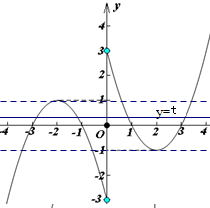
∴设函数解析式为f（x）=a（x-1）（x-3），（a≠0），
由点（0，3）在抛物线上，得
f（0）=a×（-1）×（-3）=3a=3，解之得a=1．．
∴当x＞0时，f（x）=x2-4x+3；
当x＜0时，则-x＞0，可得f（-x）=（-x）2-4（-x）+3=x2+4x+3，
∵f（x）是奇函数，∴当x＞0时，f（x）=-f（-x）=-x2-4x-3，
结合当x=0时，f（0）=0，可得f(x)=
．
（2）由函数的图象，可得函数的单调增区间为（-∞，-2]和[2，+∞）；函数的单调减区间为[-2，0）和（0，2]．
（3）由A={（x，y）|y=f（x）}，B={（x，y）|y=t，x∈R，t∈R}，
可得A∩B的元素的个数，即为直线y=t与函数y=f（x）图象公共点的个数．
∵当x＞0时，f（x）=x2-4x+3在x=2时有最小值-1；当x＞0时，f（x）=-x2-4x-3在x=-2时有最大值1
∴根据函数y=f（x）的图象，平移直线y=t可得
①当t＞1或t＜-1时，直线y=t与函数图象有2个公共点；
②当t=±1时，直线y=t与函数图象有3个公共点；
③当t=0时，直线y=t与函数图象有5个公共点；
④当-1＜t＜1且t≠0时，直线y=t与函数图象有4个公共点
由此可得满足A∩B有4个元素的实数t的取值范围为（-1，0）∪（0，1）．
∵当x＞0时，抛物线经过点（1，0）、（3，0），
∴设函数解析式为f（x）=a（x-1）（x-3），（a≠0），
由点（0，3）在抛物线上，得
f（0）=a×（-1）×（-3）=3a=3，解之得a=1．．
∴当x＞0时，f（x）=x2-4x+3；
当x＜0时，则-x＞0，可得f（-x）=（-x）2-4（-x）+3=x2+4x+3，
∵f（x）是奇函数，∴当x＞0时，f（x）=-f（-x）=-x2-4x-3，
结合当x=0时，f（0）=0，可得f(x)=
|
（2）由函数的图象，可得函数的单调增区间为（-∞，-2]和[2，+∞）；函数的单调减区间为[-2，0）和（0，2]．
（3）由A={（x，y）|y=f（x）}，B={（x，y）|y=t，x∈R，t∈R}，
可得A∩B的元素的个数，即为直线y=t与函数y=f（x）图象公共点的个数．
∵当x＞0时，f（x）=x2-4x+3在x=2时有最小值-1；当x＞0时，f（x）=-x2-4x-3在x=-2时有最大值1
∴根据函数y=f（x）的图象，平移直线y=t可得
①当t＞1或t＜-1时，直线y=t与函数图象有2个公共点；
②当t=±1时，直线y=t与函数图象有3个公共点；
③当t=0时，直线y=t与函数图象有5个公共点；
④当-1＜t＜1且t≠0时，直线y=t与函数图象有4个公共点
由此可得满足A∩B有4个元素的实数t的取值范围为（-1，0）∪（0，1）．
点评：本题给出奇函数在x＞0时的图象，求函数的表达式并讨论函数的单调性．着重考查了函数的奇偶性、单调性和函数解析式的求法等知识，属于中档题．
练习册系列答案
相关题目