题目内容
已知双曲线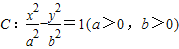 的左、右顶点分别为A、B,右焦点为F(
的左、右顶点分别为A、B,右焦点为F( ,0),
,0),一条渐近线的方程为
 ,点P为双曲线上不同于A、B的任意一点,过P作x轴的垂线交双曲线于另一点Q.
,点P为双曲线上不同于A、B的任意一点,过P作x轴的垂线交双曲线于另一点Q.(I)求双曲线C的方程;
(Ⅱ)求直线AP与直线BQ的交点M的轨迹E的方程;
(Ⅲ)过点N(l,0)作直线l与(Ⅱ)中轨迹E交于不同两点R、S,已知点T(2,0),设
 的取值范围.
的取值范围.
【答案】分析:(I)利用双曲线的右焦点为F(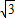 ,0),一条渐近线的方程为
,0),一条渐近线的方程为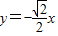 ,结合c2=a2+b2,可求双曲线C的方程;(Ⅱ)由A,M,P三点共线、B,M,Q三点共线,确定坐标之间的关系,利用双曲线方程,可得直线AP与直线BQ的交点M的轨迹E的方程;
,结合c2=a2+b2,可求双曲线C的方程;(Ⅱ)由A,M,P三点共线、B,M,Q三点共线,确定坐标之间的关系,利用双曲线方程,可得直线AP与直线BQ的交点M的轨迹E的方程;
(Ⅲ)①若直线l的斜率为0,不满足;
②当直线l的斜率不为0时,设方程为x=ty+1,代入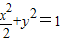 ,利用韦达定理,及
,利用韦达定理,及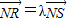 ,
,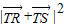 =[t(y1+y2)-2]2+(y1+y2)2=16-
=[t(y1+y2)-2]2+(y1+y2)2=16-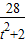 +
+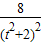 ,即可求得结论.
,即可求得结论.
解答:解:(I)∵双曲线的右焦点为F(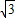 ,0),一条渐近线的方程为
,0),一条渐近线的方程为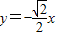 ,
,
∴c=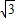 ,
,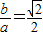
∵c2=a2+b2,∴a=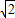 ,b=1
,b=1
∴双曲线C的方程为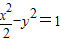 ;
;
(Ⅱ)设P(x,y),Q(x,-y),M(x,y),A(-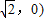 ,B(
,B(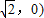
由A,M,P三点共线得:(x+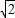 )y=y(x+
)y=y(x+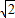 )
)
由B,M,Q三点共线得:(x- )y=-y(x-
)y=-y(x-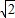 )
)
∴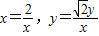
∵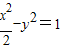
∴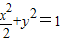
∴直线AP与直线BQ的交点M的轨迹E的方程为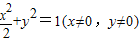 ;
;
(Ⅲ)①若直线l的斜率为0,则R(-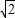 ,0),S(
,0),S(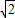 ,0),N(1,0),
,0),N(1,0),
∴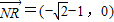 ,
,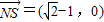
∴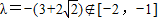
②当直线l的斜率不为0时,设方程为x=ty+1,代入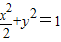 ,可得(t2+2)y2+2ty-1=0
,可得(t2+2)y2+2ty-1=0
设R(x1,y1),S(x2,y2)(y1≠0,y2≠0),则y1+y2=-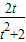 ,y1y2=-
,y1y2=-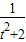
∵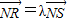 ,∴y1=λy2,∴λ=
,∴y1=λy2,∴λ=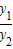 ,λ<0
,λ<0
∴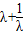 +2=
+2=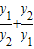 +2=
+2=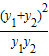 =-
=-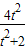
∵λ∈[-2,-1]
∴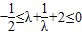
∴- ≤-
≤-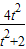 ≤0
≤0
∴0≤t2≤
∴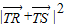 =[t(y1+y2)-2]2+(y1+y2)2=16-
=[t(y1+y2)-2]2+(y1+y2)2=16-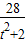 +
+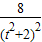
令n=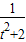 ,则n∈[
,则n∈[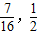 ]
]
∴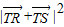 =8n2-28n+16=8(n-
=8n2-28n+16=8(n- )2-
)2-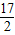
∴n= 时,
时,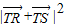 min=4;n=
min=4;n=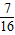 时,
时,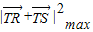 =
=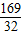
∴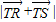 ∈[2,
∈[2,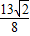 ].
].
点评:本题考查双曲线的方程,考查轨迹方程,考查向量知识的运用,考查韦达定理,考查学生的计算能力,综合性强.
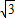 ,0),一条渐近线的方程为
,0),一条渐近线的方程为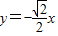 ,结合c2=a2+b2,可求双曲线C的方程;(Ⅱ)由A,M,P三点共线、B,M,Q三点共线,确定坐标之间的关系,利用双曲线方程,可得直线AP与直线BQ的交点M的轨迹E的方程;
,结合c2=a2+b2,可求双曲线C的方程;(Ⅱ)由A,M,P三点共线、B,M,Q三点共线,确定坐标之间的关系,利用双曲线方程,可得直线AP与直线BQ的交点M的轨迹E的方程;(Ⅲ)①若直线l的斜率为0,不满足;
②当直线l的斜率不为0时,设方程为x=ty+1,代入
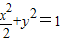 ,利用韦达定理,及
,利用韦达定理,及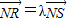 ,
,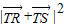 =[t(y1+y2)-2]2+(y1+y2)2=16-
=[t(y1+y2)-2]2+(y1+y2)2=16-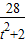 +
+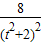 ,即可求得结论.
,即可求得结论.解答:解:(I)∵双曲线的右焦点为F(
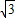 ,0),一条渐近线的方程为
,0),一条渐近线的方程为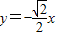 ,
,∴c=
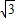 ,
,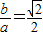
∵c2=a2+b2,∴a=
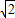 ,b=1
,b=1∴双曲线C的方程为
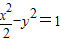 ;
;(Ⅱ)设P(x,y),Q(x,-y),M(x,y),A(-
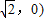 ,B(
,B(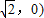
由A,M,P三点共线得:(x+
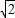 )y=y(x+
)y=y(x+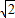 )
)由B,M,Q三点共线得:(x-
 )y=-y(x-
)y=-y(x-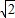 )
)∴
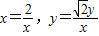
∵
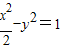
∴
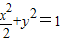
∴直线AP与直线BQ的交点M的轨迹E的方程为
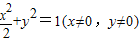 ;
;(Ⅲ)①若直线l的斜率为0,则R(-
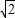 ,0),S(
,0),S(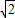 ,0),N(1,0),
,0),N(1,0),∴
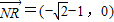 ,
,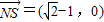
∴
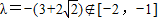
②当直线l的斜率不为0时,设方程为x=ty+1,代入
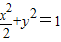 ,可得(t2+2)y2+2ty-1=0
,可得(t2+2)y2+2ty-1=0设R(x1,y1),S(x2,y2)(y1≠0,y2≠0),则y1+y2=-
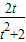 ,y1y2=-
,y1y2=-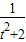
∵
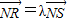 ,∴y1=λy2,∴λ=
,∴y1=λy2,∴λ=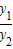 ,λ<0
,λ<0∴
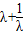 +2=
+2=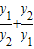 +2=
+2=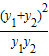 =-
=-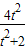
∵λ∈[-2,-1]
∴
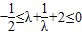
∴-
 ≤-
≤-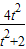 ≤0
≤0∴0≤t2≤

∴
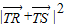 =[t(y1+y2)-2]2+(y1+y2)2=16-
=[t(y1+y2)-2]2+(y1+y2)2=16-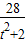 +
+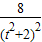
令n=
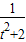 ,则n∈[
,则n∈[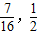 ]
]∴
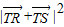 =8n2-28n+16=8(n-
=8n2-28n+16=8(n- )2-
)2-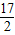
∴n=
 时,
时,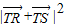 min=4;n=
min=4;n=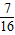 时,
时,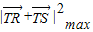 =
=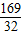
∴
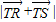 ∈[2,
∈[2,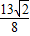 ].
].点评:本题考查双曲线的方程,考查轨迹方程,考查向量知识的运用,考查韦达定理,考查学生的计算能力,综合性强.

练习册系列答案
相关题目
 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.  与
与 交点的轨迹E的方程
交点的轨迹E的方程 的两条直线
的两条直线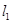 和
和 与轨迹E都只有一个交点,且
与轨迹E都只有一个交点,且 ,求
,求 的值.
的值. 分)
分) 的左、 右顶点分别为
的左、 右顶点分别为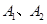 ,动直线
,动直线 与圆
与圆 相切,且与双曲线左、右两支的交点分别为
相切,且与双曲线左、右两支的交点分别为 .
.
 的取值范围,并求
的取值范围,并求 的最小值;
的最小值; 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为 ,那么,
,那么, 是定值吗?并证明
是定值吗?并证明 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
,则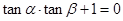 B、
B、
 D、
D、
 的左、右顶点分别为
的左、右顶点分别为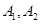 ,点
,点 ,
, 是双曲线上不同的两个动点.
是双曲线上不同的两个动点.  与
与 交点的轨迹E的方程
交点的轨迹E的方程 和
和 与轨迹E都只有一个公共点,且
与轨迹E都只有一个公共点,且 ,求
,求 的值.
的值. 的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P,
的左、右顶点分别为A、B,双曲线在第一象限的图象上有一点P, ,则
( )
,则
( ) B.
B.
 D.
D.