题目内容
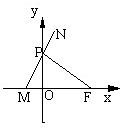 如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|.
如图,已知定点F(1,0),动点P在y轴上运动,过点P作PM⊥PF并交x轴于M点,延长MP到N,使|PN|=|PM|.(1)求动点N的轨迹C的方程;
(2)直线l与动点N的轨迹C交于A、B两点,若
| OA |
| OB |
| 6 |
| 30 |
分析:(1)设出动点N,则M,P的坐标可表示出,利用PM⊥PF,kPMkPF=-1,求得x和y的关系式,即N的轨迹方程.
(2)设出直线l的方程,A,B的坐标,根据
•
=-4,推断出x1x2+y1y2=-4进而求得y1y2的值,把直线与抛物线方程联立消去x求得y1y2的表达式,进而气的b和k的关系式,利用弦长公式表示出|AB|2,根据|AB|的范围,求得k的范围.
(2)设出直线l的方程,A,B的坐标,根据
| OA |
| OB |
解答:解:(1)设动点N(x,y),则M(-x,0),P(0,
)(x>0)
∵PM⊥PF,∴kPMkPF=-1,即
•
=-1,∴y2=4x(x>0)即为所求.
(2)设直线l方程为y=kx+b,l与抛物线交于点A(x1,y1)、B(x2,y2),
则由
•
=-4,得x1x2+y1y2=-4,即
+y1y2=-4,∴y1y2=-8,
由
?ky2-4y+4b=0(其中k≠0),∴y1y2=
=-8,b=-2k,
当△=16-16kb=16(1+2k2)>0时,
|AB|2=(1+
)(y2-y1)2=
[(y1+y2)2-4(y1y2)]=
(
+32)
由题意,得16×6≤
(
+32)≤16×30
解得,
≤k2≤1,
≤k≤1或-1≤k≤-
,
即所求k的取值范围是[-1,-
]∪[
,1].
| y |
| 2 |
∵PM⊥PF,∴kPMkPF=-1,即
| ||
| x |
| ||
| -1 |
(2)设直线l方程为y=kx+b,l与抛物线交于点A(x1,y1)、B(x2,y2),
则由
| OA |
| OB |
| y12y22 |
| 16 |
由
|
| 4b |
| k |
当△=16-16kb=16(1+2k2)>0时,
|AB|2=(1+
| 1 |
| k2 |
| 1+k2 |
| k2 |
| 1+k2 |
| k2 |
| 16 |
| k2 |
由题意,得16×6≤
| 1+k2 |
| k2 |
| 16 |
| k2 |
解得,
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
即所求k的取值范围是[-1,-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查运用解析几何的方法分析问题和解决问题的能力.

练习册系列答案
相关题目
 (2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4
(2011•潍坊二模)如图,已知定点F(-1,0),N(1,0),以线段FN为对角线作周长是4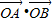 =-4,且
=-4,且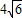 ≤|AB|≤
≤|AB|≤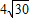 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.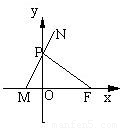
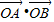 =-4,且
=-4,且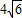 ≤|AB|≤
≤|AB|≤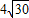 ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.
 =-4,且
=-4,且 ≤|AB|≤
≤|AB|≤ ,求直线l的斜率的取值范围.
,求直线l的斜率的取值范围.