题目内容
附加题
已知函数f(x)=log2
(Ⅰ)求f(x)的定义域;
(Ⅱ)讨论f(x)的奇偶性;
(Ⅲ)求使f(x)>0的x的取值范围.
已知函数f(x)=log2
| 2+x | 2-x |
(Ⅰ)求f(x)的定义域;
(Ⅱ)讨论f(x)的奇偶性;
(Ⅲ)求使f(x)>0的x的取值范围.
分析:(I)求对数函数的定义域,根据真数大于等于0建立关系式,然后解分式不等式即可.
(II)利用奇偶性的定义,看f(-x)和f(x)的关系,注意到
和
互为倒数,其对数值互为相反数,也可计算f(-x)+f(x)=0得到.
(III)解对数不等式,注意定义域是前提.
(II)利用奇偶性的定义,看f(-x)和f(x)的关系,注意到
| 2+x |
| 2-x |
| 2-x |
| 2+x |
(III)解对数不等式,注意定义域是前提.
解答:解:(I)由对数函数的定义知
>0.
如果
,则-2<x<2;
如果
,则不等式组无解.
故f(x)的定义域为(-2,2)
(II)∵f(-x)=log2
=-log2
=-f(x),
∴f(x)为奇函数.
(III)log2
>0等价于
>1,①
而从(I)知2-x>0,故①等价于2+x>2-x,又等价于x>0.
∴当x∈(0,2)时有f(x)>0
| 2+x |
| 2-x |
如果
|
如果
|
故f(x)的定义域为(-2,2)
(II)∵f(-x)=log2
| 2-x |
| 2+x |
| 2+x |
| 2-x |
∴f(x)为奇函数.
(III)log2
| 2+x |
| 2-x |
| 2+x |
| 2-x |
而从(I)知2-x>0,故①等价于2+x>2-x,又等价于x>0.
∴当x∈(0,2)时有f(x)>0
点评:本题主要考查了对数函数的性质:定义域、奇偶性、单调性等有关知识,同时考查了转化的思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
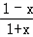 ,其中a>0.
,其中a>0.