题目内容
已知函数f(x)=ln(x+a),g(x)= x3+b,直线l:y=x与y=f(x)相切,
x3+b,直线l:y=x与y=f(x)相切,
(1)求a的值
(2)若方程f(x)=g(x)在(0,+∞)上有且仅有两个解x1,x2求b的取值范围,并比较x1x2+1与x1+x2的大小.(3)设n≥2时,n∈N*,求证:
 +…
+… <1
<1
解:(1)设切(x0,y0),y0=x0,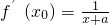 ,
,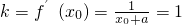
∴x0+a=1,且y0=ln(x0+a)=0,∴x0=0,a=1(3分)
(2)ln(x+a)=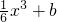 ,得
,得
令h(x)= ,
,
在(0,1)上h′(x)<0,故h(x)在(0,1)单调减
在(1,+∞)上,h′(x)>0,故h(x)在(1,+∞)单调增
∴ ,若h(x)图在(0,+∞)内x轴有两个不同的交点,则
,若h(x)图在(0,+∞)内x轴有两个不同的交点,则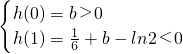
,此时h(3)=
所b的范围为 .(8分)
.(8分)
由上知,方程f(x)=g(x)在(0,+∞)上有且仅有两个x1、x2,满足0<x1<1,x2>1,
∴x1x2+1-(x1+x2)=(1-x1)(1-x2)<0
∴x1x2+1<(x1+x2)
(3)求导数可证f(x)≤x,即ln(x+1)≤x(10分)
故n≥2,n∈N*时,lnn<n-1
∴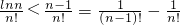 (12分)
(12分)
∴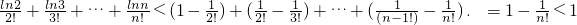 (13分)
(13分)
分析:(1)考查导数的几何意义,方程思想解决
(2)考查构建函数,利用导数求函数范围,利用图象数形结合列式求解
(3)考查利用导数证明不等式,构建函数能力
点评:本题考查导数的综合应用,对学生的能力要求较大,属于难题
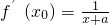 ,
,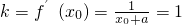
∴x0+a=1,且y0=ln(x0+a)=0,∴x0=0,a=1(3分)
(2)ln(x+a)=
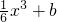 ,得
,得
令h(x)=
 ,
,
在(0,1)上h′(x)<0,故h(x)在(0,1)单调减
在(1,+∞)上,h′(x)>0,故h(x)在(1,+∞)单调增
∴
 ,若h(x)图在(0,+∞)内x轴有两个不同的交点,则
,若h(x)图在(0,+∞)内x轴有两个不同的交点,则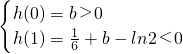
,此时h(3)=

所b的范围为
 .(8分)
.(8分)由上知,方程f(x)=g(x)在(0,+∞)上有且仅有两个x1、x2,满足0<x1<1,x2>1,
∴x1x2+1-(x1+x2)=(1-x1)(1-x2)<0
∴x1x2+1<(x1+x2)
(3)求导数可证f(x)≤x,即ln(x+1)≤x(10分)
故n≥2,n∈N*时,lnn<n-1
∴
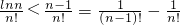 (12分)
(12分)∴
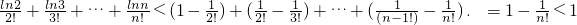 (13分)
(13分)分析:(1)考查导数的几何意义,方程思想解决
(2)考查构建函数,利用导数求函数范围,利用图象数形结合列式求解
(3)考查利用导数证明不等式,构建函数能力
点评:本题考查导数的综合应用,对学生的能力要求较大,属于难题

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目