题目内容
((本小题满分12分)
设函数 ,且
,且 ,其中
,其中 是自然对数的底数.
是自然对数的底数.
(I)求 与
与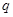 的关系;
的关系;
(II)若 在其定义域内为单调函数,求
在其定义域内为单调函数,求 的取值范围
的取值范围
【答案】
(Ⅰ)证明:由题设 ,得
,得 ,即
,即 .
.
又 ,所以数列
,所以数列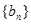 是其首项为3,且公比为2等比数列.……6分
是其首项为3,且公比为2等比数列.……6分
(Ⅱ)解:由(1)知, .……8分
.……8分
于是 .………………………9分
.………………………9分
所以
 .……………………………10分
.……………………………10分
所以

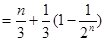
 .……………12分
.……………12分
21.解:(I)由题意得

而 ,所以
,所以 、
、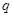 的关系为
的关系为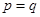 ……4分
……4分
(II)由(I)知 ,
,
 ……6分
……6分

②当 >0时,
>0时, ,其图像为开口向上的抛物线,对称轴为
,其图像为开口向上的抛物线,对称轴为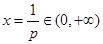 ,
,
∴ ,
,
只需 ,即
,即 ,
,
∴ 在
在 内为单调递增函数,
内为单调递增函数,
故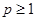 适合题意. ……10分
适合题意. ……10分
③当 <0时,
<0时, ,其图像为开口向下的抛物线,对称轴为
,其图像为开口向下的抛物线,对称轴为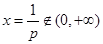 ,只要
,只要 ,
,
即 时,
时, 在
在 恒成立,故
恒成立,故 <0适合题意.
<0适合题意.
综上所述, 的取值范围为
的取值范围为 . ……12分
. ……12分
【解析】略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目