题目内容
已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时, ![]() (其中e是自然界对数的底,
(其中e是自然界对数的底, ![]() )
)
(1) 求![]() 的解析式;
的解析式;
(2) 设![]() ,求证:当
,求证:当![]() ,
,![]() 时,
时,![]() ;
;
(3)是否存在负数a,使得当![]() 时,
时,![]() 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
![]() ,存在负数
,存在负数![]()
解析:
解:(1)设![]() ,则
,则![]() ,所以
,所以![]()
又因为![]() 是定义在
是定义在![]() 上的奇函数,所以
上的奇函数,所以![]()
故函数![]() 的解析式为
的解析式为![]()
(2)证明:当![]() 且
且![]() 时,
时,![]() ,设
,设![]()
因为![]() ,所以当
,所以当![]() 时,
时,![]() ,此时
,此时![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递增,所以
单调递增,所以![]()
又因为![]() ,所以当
,所以当![]() 时,
时,![]() ,此时
,此时![]() 单调递减,
单调递减,
所以![]()
所以当![]() 时,
时,![]() 即
即![]()
(3)解:假设存在负数![]() ,使得当
,使得当![]() 时,
时,![]() 有最小值是3,则
有最小值是3,则![]()
①当![]() ,由于
,由于![]() ,则
,则![]() ,
,
故函数![]() 是
是![]() 上的增函数.
上的增函数.
所以![]() ,解得
,解得![]() (舍去)
(舍去)
②当![]() 时,则
时,则
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 是减函数;
是减函数;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 是增函数.
是增函数.
所以![]() ,解得
,解得![]() 满足题意。
满足题意。
综上可知,存在负数![]() ,使得当
,使得当![]() 时,
时,![]() 有最小值3
有最小值3

练习册系列答案
相关题目
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。 的解析式;
的解析式; 。
。 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
, 的解析式;
的解析式;
 是定义在
是定义在 上的以5为周期的奇函数, 若
上的以5为周期的奇函数, 若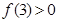 ,
, ,则a的取值范围是 ( )
,则a的取值范围是 ( )  B.
B.

 D.
D.

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )
) ,求证:当
,求证:当 时,
时, ;
; 时,
时, 是定义在
是定义在 上的奇函数,且
上的奇函数,且
 的解析式;
的解析式; 的单调性;
的单调性;