题目内容
.圆C的半径为3,圆心C在直线2x+y=0上且在x轴的下方,x轴被圆C截得的弦长BD为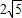 .
.(1)求圆C的方程;
(2)若圆E与圆C关于直线2x-4y+5=0对称,试判断两圆的位置关系.
【答案】分析:(1)由题意可设方程为(x-a)2+(y+2a)2=9,由条件可得a=1,进而可得方程;(2)设圆心E(m,n),由对称关系可得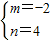 ,半径为3,可得
,半径为3,可得 ,故相离.
,故相离.
解法二,先得圆C与直线2x-4y+5=0相离,进而可得对称的圆与已知圆相离.
解答:解:(1)由题意设圆心坐标(a,-2a)---(1分),则圆方程为(x-a)2+(y+2a)2=9----(2分)
作CA⊥x轴于点A,在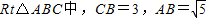 ,∴CA=2,-------(4分)
,∴CA=2,-------(4分)
所以|-2a|=2,解得a=±1-----------(5分)
又因为点C在x轴的下方,所以a=1,即C(1,-2)-----------(6分)
所以圆方程为:(x-1)2+(y+2)2=9------------(7分)
(2)设圆心E(m,n),由题意可知点E与点C是关于直线2x-4y+5=0对称,
所以有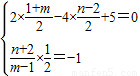 --------(9分)可解得
--------(9分)可解得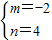 -------------(11分)
-------------(11分)
所以点E(-2,4)且圆E的半径为3--------(12分)
所以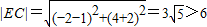 ,----(13分)
,----(13分)
故两圆为相离关系---------------(14分)
解法二:点C(1.-2)到直线的距离为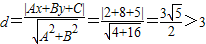 -------(9分)
-------(9分)
所以圆C与直线2x-4y+5=0相离-----(11分)
而圆E与圆C关于直线2x-4y+5=0对称,
所以圆E与直线2x-4y+5=0也相离,------(13分)
故两圆相离.-------(14分)
点评:本题考查直线和圆的位置关系,以及对称问题,属中档题.
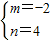 ,半径为3,可得
,半径为3,可得 ,故相离.
,故相离.解法二,先得圆C与直线2x-4y+5=0相离,进而可得对称的圆与已知圆相离.
解答:解:(1)由题意设圆心坐标(a,-2a)---(1分),则圆方程为(x-a)2+(y+2a)2=9----(2分)
作CA⊥x轴于点A,在
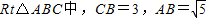 ,∴CA=2,-------(4分)
,∴CA=2,-------(4分)所以|-2a|=2,解得a=±1-----------(5分)
又因为点C在x轴的下方,所以a=1,即C(1,-2)-----------(6分)
所以圆方程为:(x-1)2+(y+2)2=9------------(7分)
(2)设圆心E(m,n),由题意可知点E与点C是关于直线2x-4y+5=0对称,
所以有
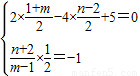 --------(9分)可解得
--------(9分)可解得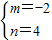 -------------(11分)
-------------(11分)所以点E(-2,4)且圆E的半径为3--------(12分)
所以
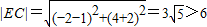 ,----(13分)
,----(13分)故两圆为相离关系---------------(14分)
解法二:点C(1.-2)到直线的距离为
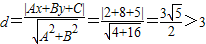 -------(9分)
-------(9分)所以圆C与直线2x-4y+5=0相离-----(11分)
而圆E与圆C关于直线2x-4y+5=0对称,
所以圆E与直线2x-4y+5=0也相离,------(13分)
故两圆相离.-------(14分)
点评:本题考查直线和圆的位置关系,以及对称问题,属中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴相切,则该圆的标准方程是( )
A、(x-3)2+(y-
| ||
| B、(x-2)2+(y-1)2=1 | ||
| C、(x-1)2+(y-3)2=1 | ||
D、(x-
|