题目内容
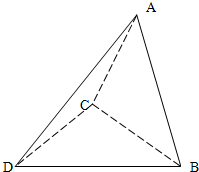 三棱锥A-BCD,其中△BCD为直角三角形,∠BDC=90°,AB=AC=AD=5,BD=4,CD=4
三棱锥A-BCD,其中△BCD为直角三角形,∠BDC=90°,AB=AC=AD=5,BD=4,CD=4| 3 |
(1)求证:面BCD⊥面ABC
(2)求二面角C-AD-B的平面角.
分析:(1)取BC中点O,连接DO,有已知条件可得△AOB≌△AOC≌△AOD,进而得到∠AOB=∠AOC=∠AOD=90°;从而有AO⊥面BCD可得面BCD⊥面ABC;
(2)过O作OF与BC垂直,交CD于F点,建立空间直角坐标系,求出个对应点的坐标,进而求出面ACD的法向量以及面ABD的法向量的坐标,最后代入向量夹角的计算公式即可得到结论.
(2)过O作OF与BC垂直,交CD于F点,建立空间直角坐标系,求出个对应点的坐标,进而求出面ACD的法向量以及面ABD的法向量的坐标,最后代入向量夹角的计算公式即可得到结论.
解答: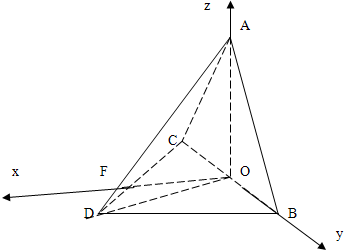 (1)证明:取BC中点O,连接DO,由已知△BCD为直角三角形,可得OC=OD=OB,
(1)证明:取BC中点O,连接DO,由已知△BCD为直角三角形,可得OC=OD=OB,
又知AB=AC=AD,则△AOB≌△AOC≌△AOD,(2分)
可知∠AOB=∠AOC=∠AOD=90°,
则AO⊥面BCD,AO?面ABC
得面BCD⊥面ABC(6分)
(2)解:过O作OF与BC垂直,交CD于F点,
建系[O;
,
,
]
则 A(0,0,4),B(0,4,0),
C (0,-4,0),D(2
,2,0)(8分)
设面ACD的法向量为
=(x,y,z),由
•
=0,
•
=0,可知
=(-3
,3,-4)
设面ABD的法向量为
=(x,y,z),由
•
=0,
•
=0,可知
=(
,3,4)(12分)
∴cos<n1,n2>=-
,
则<n1,n2>=π-arccos
(14分)
 (1)证明:取BC中点O,连接DO,由已知△BCD为直角三角形,可得OC=OD=OB,
(1)证明:取BC中点O,连接DO,由已知△BCD为直角三角形,可得OC=OD=OB,又知AB=AC=AD,则△AOB≌△AOC≌△AOD,(2分)
可知∠AOB=∠AOC=∠AOD=90°,
则AO⊥面BCD,AO?面ABC
得面BCD⊥面ABC(6分)
(2)解:过O作OF与BC垂直,交CD于F点,
建系[O;
| OF, |
| OB |
| OA |
则 A(0,0,4),B(0,4,0),
C (0,-4,0),D(2
| 3 |
设面ACD的法向量为
| n1 |
| n1 |
| AC |
| n1 |
| AD |
| n1 |
| 3 |
设面ABD的法向量为
| n2 |
| n2 |
| AB |
| n2 |
| AD |
| n1 |
| 3 |
∴cos<n1,n2>=-
4
| ||
| 91 |
则<n1,n2>=π-arccos
4
| ||
| 91 |
点评:本题主要考察用空间向量求平面间的夹角以及线面垂直的证明.在用空间向量求平面间的夹角问题时,一定要注意平面的法向量不能求错.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
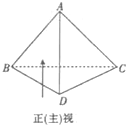 如图,三棱锥A-BCD的底面为正三角形,侧面ABC与底面垂直且 AB=AC,已知其正(主)视图的面积为2,则其侧(左)视图的面积为( )
如图,三棱锥A-BCD的底面为正三角形,侧面ABC与底面垂直且 AB=AC,已知其正(主)视图的面积为2,则其侧(左)视图的面积为( )