题目内容
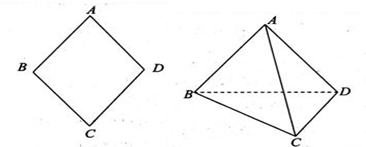
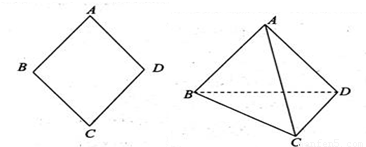
如图所示,已知菱形ABCD的边长为2,将其沿对角线BD折成直二面角A-BD-C.
(1)证明:AC⊥BD;
(2)若二面角A-BC-D的平面角的正切值为2,求三棱锥A-BCD的体积.

(1)证明:AC⊥BD;
(2)若二面角A-BC-D的平面角的正切值为2,求三棱锥A-BCD的体积.
分析:(1)取BD中点O,连接AO,CO,则AO⊥BD,CO⊥BD,可得BD⊥平面AOC,从而可得AC⊥BD;
(2)过O作OE⊥BC于E,连接AE,则∠AEO为二面角A-BC-D的平面角,利用二面角A-BC-D的平面角的正切值为2,可得AO=CO=
,BD=2,从而可求三棱锥A-BCD的体积.
(2)过O作OE⊥BC于E,连接AE,则∠AEO为二面角A-BC-D的平面角,利用二面角A-BC-D的平面角的正切值为2,可得AO=CO=
| 3 |
解答: (1)证明:取BD中点O,连接AO,CO,则AO⊥BD,CO⊥BD
(1)证明:取BD中点O,连接AO,CO,则AO⊥BD,CO⊥BD
∵AO∩CO=O,
∴BD⊥平面AOC,
∵AC?平面AOC,
∴AC⊥BD;
(2)解:过O作OE⊥BC于E,连接AE,则AO⊥面BCD,∴AO⊥BC
∵OE∩AO=O,∴BC⊥面AEO
∴∠AEO为二面角A-BC-D的平面角
∵二面角A-BC-D的平面角的正切值为2
∴
=2
∴OE=
AO=
CO
∴∠OCB=30°
∴∠BCD=60°
∴AO=CO=
,BD=2
∴三棱锥A-BCD的体积为V=
×
×2×
×
=1.
 (1)证明:取BD中点O,连接AO,CO,则AO⊥BD,CO⊥BD
(1)证明:取BD中点O,连接AO,CO,则AO⊥BD,CO⊥BD∵AO∩CO=O,
∴BD⊥平面AOC,
∵AC?平面AOC,
∴AC⊥BD;
(2)解:过O作OE⊥BC于E,连接AE,则AO⊥面BCD,∴AO⊥BC
∵OE∩AO=O,∴BC⊥面AEO
∴∠AEO为二面角A-BC-D的平面角
∵二面角A-BC-D的平面角的正切值为2
∴
| AO |
| OE |
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OCB=30°
∴∠BCD=60°
∴AO=CO=
| 3 |
∴三棱锥A-BCD的体积为V=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查线面垂直,线线垂直,考查三棱锥的体积,掌握线面垂直的判定,正确利用三棱锥的体积公式是关键.

练习册系列答案
相关题目
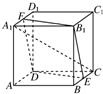 如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点.
如图所示,已知正方体ABCD-A1B1C1D1的棱长为a,E,F分别是BC,A1D1的中点. 如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )
如图所示,已知点P为菱形ABCD外一点,且PA⊥面ABCD,PA=AD=AC,点F为PC中点,则二面角CBFD的正切值为( )