题目内容
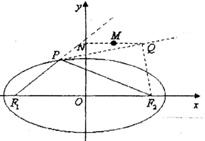 如图,已知椭圆
如图,已知椭圆| x2 | 4 |
分析:点F2关于∠F1PF2的外角平分线PQ的对称点Q′在直线F1P的延长线上,故|F1Q′|=|PF1|+|PF2|=2a(椭圆长轴长),又OQ是△F2F1Q′的中位线,故|OQ|=a,由此可以求点M的轨迹方程.
解答:解:点F2关于∠F1PF2的外角平分线PQ的对称点Q′在直线F1P的延长线上,故|F1Q′|=|PF1|+|PF2|=2a(椭圆长轴长),
又OQ是△F2F1Q′的中位线,故|OQ|=2,
设M(x,y),则Q(2x,y),
所以有4x2+y2=4,
故答案为
+x2=1.
又OQ是△F2F1Q′的中位线,故|OQ|=2,
设M(x,y),则Q(2x,y),
所以有4x2+y2=4,
故答案为
| y2 |
| 4 |
点评:本题主要应用角分线的性质解决问题,从而转化为利用椭圆的定义,同时解题中利用了代入法求轨迹方程.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
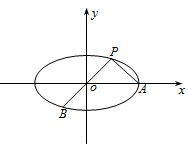 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆
如图,已知椭圆 (2010•武昌区模拟)如图,已知椭圆
(2010•武昌区模拟)如图,已知椭圆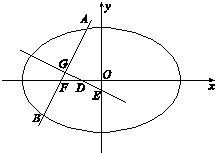 (2013•甘肃三模)如图,已知椭圆
(2013•甘肃三模)如图,已知椭圆