题目内容
 如图,已知椭圆
如图,已知椭圆| x2 |
| 4 |
| π-2 |
| 4π |
| π-2 |
| 4π |
(椭圆的面积公式S=π•a•b,其中a是椭圆长半轴长,b是椭圆短半轴长)
分析:先根据椭圆的面积公式S=π•a•b求出椭圆面积,然后利用四分之一个椭圆减去直角三角形的面积求出阴影部分面积,最后根据几何概型的概率公式解之即可.
解答:解:∵
+y2=1,
∴a=2,b=1则椭圆的面积S=π•a•b=2π,
∵图中阴影的面积为
-
×2×1=
-1
∴豆子落在图中阴影范围内的概率为
=
故答案为:
| x2 |
| 4 |
∴a=2,b=1则椭圆的面积S=π•a•b=2π,
∵图中阴影的面积为
| S |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
∴豆子落在图中阴影范围内的概率为
| ||
| 2π |
| π-2 |
| 4π |
故答案为:
| π-2 |
| 4π |
点评:本题主要考查了几何概型,以及椭圆的面积,同时考查了利用间接法求阴影部分面积,属于基础题.

练习册系列答案
相关题目
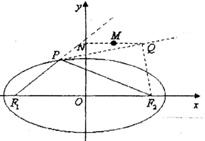 如图,已知椭圆
如图,已知椭圆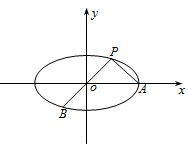 如图,已知椭圆
如图,已知椭圆 (2010•武昌区模拟)如图,已知椭圆
(2010•武昌区模拟)如图,已知椭圆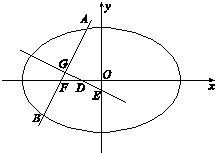 (2013•甘肃三模)如图,已知椭圆
(2013•甘肃三模)如图,已知椭圆