题目内容
已知函数
在
处取得极值．
（1)讨论
和
是函数
的极大值还是极小值；
（2）过点
作曲线
的切线，求此切线方程．
（1）
是极小值，
是极大值．（2）切线方程为：
解析:
（1）
由于
在
处取得极值
所以：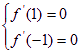
即：
解得：
所以：
当
时，
，此时为增函数；
当
时，
，此时为减函数．
所以是极小值，是极大值．
（2）设切点为
由题意得：
解得：
所以切线的斜率为
所以过点（0，16）的切线方程为：
练习册系列答案
阅读快车系列答案
相关题目
在
处取得极值.
；
，如果
在开区间
上存在极小值，求实数
的取值范围.
=
在
处取得极值.
的值；
的方程
在
上恰有两个不相等的实数根，求实数
的取值范围；
在
处取得极值。
的解析式；
上任意两个自变量的值
，都有
；
可作曲线
的三条切线，求实数
的取值范围。
为实数。
在
处取得极值，求
的值；
对任意
都成立，求实数
的取值范围。
在
处取得极值．
的值；[来源:学+科+网]
的方程
在区间
上恰有两个不同的实数根，求实数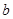
的取值范围．