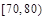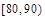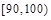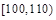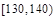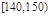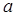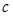Question

（本小题满分12分）

某校共有800名学生，高三一次月考之后，为了了解学生学习情况，用分层抽样方法从中抽出若干学生此次数学成绩，按成绩分组，制成如下的频率分布表：

组号	第 一 组	第 二 组	第 三 组	第 四 组	第 五 组	第 六 组	第 七 组	第 八 组	合计
分组
频数	4	6	20	22	18		10	5
频率	0.04	0.06	0.20	0.22		0.15	0.10	0.05	1

（Ⅰ）李明同学本次数学成绩为103分，求他被抽中的概率；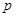

（Ⅱ）为了了解数学成绩在120分以上的学生的心理状态，现决定在第六、七、八组中用分层抽样方法抽取6名学生的成绩，并在这6名学生中在随机抽取2名由心理老师张老师负责面谈，求第七组至少有一名学生与张老师面谈的概率；

（Ⅲ）估计该校本次考试的数学平均分。

 

Answer 1

【答案】

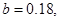
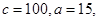 （1）；

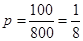（2）抽取2个的方法有ab ac ad aE aF bd bc bE bF cd cE cF dE dF EF， 共15种。

至少含E或F的取法有 9种，概率为；

（3）估计平均分为110.4分。

【解析】

试题分析：因为频率和为1 所以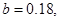                      （1分）

因为频率=频数/样本容量 所以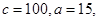         （3分）

（1）每位学生成绩被抽取的机会均等 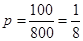           （5分）

（2） 在第六、七、八组共有30个样本，用分层抽样方法抽取6名学生的成绩，每个被抽取的概率为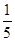。第七组被抽取的样本数为。

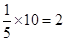将第六组、第八组抽取的样本用a,b,c,d表示，第七组抽出的样本用E,F表示。

抽取2个的方法有ab ac ad aE aF bd bc bE bF cd cE cF dE dF EF， 共15种。

至少含E或F的取法有 9种，概率为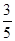                 （9分）

（3）75x0.04+85x0.06+95x0.2+105x0.22+115x0.18

+125x0.15+135x0.1+145x0.05=110.4      估计平均分为110.4分        （12分）

考点：本题主要考查抽样方法，频率的概念及计算，古典概型概率的计算。

点评：典型题，统计中的抽样方法，频率直方图，概率计算及分布列问题，是高考必考内容及题型。古典概型概率的计算问题，关键是明确基本事件数，往往借助于“树图法”，做到不重不漏。