题目内容
三棱锥S—ABC中,一条棱长为a,其余棱长均为1,求a为何值时VS—ABC最大,并求最大值.
a为![]() 时,三棱锥的体积最大为
时,三棱锥的体积最大为![]()
解析:
方法一 如图所示,
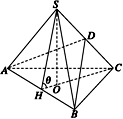 设SC=a,其余棱长均为1,
设SC=a,其余棱长均为1,
取AB的中点H,连接HS、HC,
则AB⊥HC,AB⊥HS,
∴AB⊥平面SHC.
在面SHC中,过S作SO⊥HC,则SO⊥平面ABC.
在△SAB中,SA=AB=BS=1,
∴SH=![]() ,
,
设∠SHO=![]() ,则SO=SHsin
,则SO=SHsin![]() =
=![]() sin
sin![]() ,
,
∴VS—ABC=![]() S△ABC·SO
S△ABC·SO
=![]() ×
×![]() ×12×
×12×![]() sin
sin![]()
=![]() sin
sin![]() ≤
≤![]() .
.
当且仅当sin![]() =1,即
=1,即![]() =90°时,三棱锥的体积最大.
=90°时,三棱锥的体积最大.
a=![]() SH=
SH=![]() ×
×![]() =
=![]() ,Vmax=
,Vmax=![]() .
.
∴a为![]() 时,三棱锥的体积最大为
时,三棱锥的体积最大为![]() .
.
方法二 取SC的中点D,可通过VS—ABC=![]() S△ABD·SC,转化为关于a的目标函数的最大值问题,利用基本不等式或配方法解决.
S△ABD·SC,转化为关于a的目标函数的最大值问题,利用基本不等式或配方法解决.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
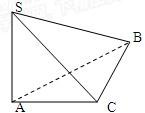 如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,
如图在三棱锥S-ABC中∠ACB=90°,SA⊥面ABC,AC=2,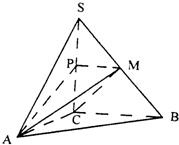 如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°.
如图,在三棱锥S-ABC中,SC⊥平面ABC,点P、M分别是SC和SB的中点,设PM=AC=1,∠ACB=90°,直线AM与直线SC所成的角为60°. 如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形,
如图,在三棱锥S-ABC中,△ABC是边长为8的正三角形, 如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2
如图,在三棱锥S-ABC中,平面SBC⊥平面ABC,SB=SC=AB=2,BC=2