题目内容
已知 的顶点
的顶点 ,
, 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 .
.
(1)求 的顶点
的顶点 、
、 的坐标;
的坐标;
(2)若圆 经过不同的三点
经过不同的三点 、
、 、
、 ,且斜率为
,且斜率为 的直线与圆
的直线与圆 相切于点
相切于点 ,求圆
,求圆 的方程.
的方程.
 的顶点
的顶点 ,
, 边上的中线
边上的中线 所在的直线方程为
所在的直线方程为 ,
, 边上的高
边上的高 所在直线的方程为
所在直线的方程为 .
.(1)求
 的顶点
的顶点 、
、 的坐标;
的坐标;(2)若圆
 经过不同的三点
经过不同的三点 、
、 、
、 ,且斜率为
,且斜率为 的直线与圆
的直线与圆 相切于点
相切于点 ,求圆
,求圆 的方程.
的方程.解:(1) 边上的高
边上的高 所在直线的方程为
所在直线的方程为 ,所以,
,所以,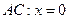 ,
,
又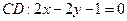 ,所以,
,所以, ,
,
设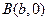 ,则
,则 的中点
的中点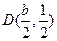 ,代入方程
,代入方程 ,
,
解得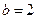 ,所以
,所以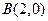 .
.
(2)由 ,
,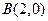 可得,圆
可得,圆 的弦
的弦 的中垂线方程为
的中垂线方程为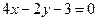 ,
,
注意到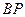 也是圆
也是圆 的弦,所以,圆心在直线
的弦,所以,圆心在直线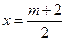 上,
上,
设圆心 坐标为
坐标为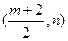 ,
,
因为圆心 在直线
在直线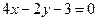 上,所以
上,所以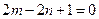 …………①,
…………①,
又因为斜率为 的直线与圆
的直线与圆 相切于点
相切于点 ,所以
,所以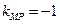 ,
,
即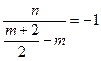 ,整理得
,整理得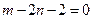 …………②,
…………②,
由①②解得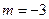 ,
,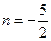 ,
,
所以,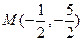 ,半径
,半径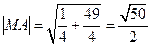 ,
,
所以所求圆方程为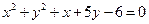
 边上的高
边上的高 所在直线的方程为
所在直线的方程为 ,所以,
,所以,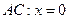 ,
,又
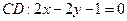 ,所以,
,所以, ,
,设
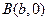 ,则
,则 的中点
的中点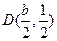 ,代入方程
,代入方程 ,
,解得
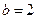 ,所以
,所以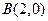 .
. (2)由
 ,
,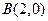 可得,圆
可得,圆 的弦
的弦 的中垂线方程为
的中垂线方程为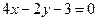 ,
,注意到
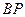 也是圆
也是圆 的弦,所以,圆心在直线
的弦,所以,圆心在直线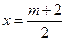 上,
上,设圆心
 坐标为
坐标为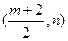 ,
,因为圆心
 在直线
在直线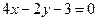 上,所以
上,所以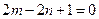 …………①,
…………①,又因为斜率为
 的直线与圆
的直线与圆 相切于点
相切于点 ,所以
,所以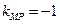 ,
,即
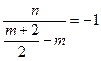 ,整理得
,整理得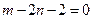 …………②,
…………②, 由①②解得
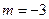 ,
,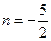 ,
,所以,
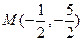 ,半径
,半径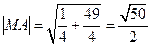 ,
,所以所求圆方程为
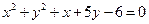
略

练习册系列答案
相关题目
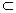 α
α 过点
过点 ,倾斜角的正弦是
,倾斜角的正弦是 ,求直线
,求直线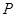 是曲线
是曲线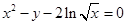 上任意一点,则点
上任意一点,则点 的
的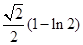
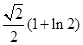
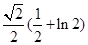
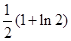
 :
: 与直线
与直线 :
: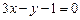 相互垂直,则实数
相互垂直,则实数 等于 ▲ .
等于 ▲ .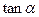 ,则此直线的倾斜角为
,则此直线的倾斜角为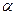 ③若一条直线的倾斜角为
③若一条直线的倾斜角为 率为
率为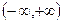

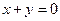 有一点
有一点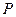 ,使它到原点的距离等于它到直线
,使它到原点的距离等于它到直线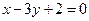 的距离,则点
的距离,则点 与抛物线
与抛物线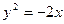 所围成平面图形的面积是 .
所围成平面图形的面积是 .