Question

【题目】（选修4﹣5：不等式选讲）
已知函数f（x）=|2x﹣1|+|2x+a|，g（x）=x+3．
（1）当a=﹣2时，求不等式f（x）＜g（x）的解集；
（2）设a＞﹣1，且当 时，f（x）≤g（x），求a的取值范围．

Answer 1

【答案】
（1）解：当a=﹣2时，求不等式f（x）＜g（x）化为|2x﹣1|+|2x﹣2|﹣x﹣3＜0．

设y=|2x﹣1|+|2x﹣2|﹣x﹣3，则 y= 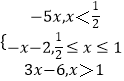，它的图象如图所示：

结合图象可得，y＜0的解集为（0，2），故原不等式的解集为（0，2）．

（2）解：设a＞﹣1，且当 时，f（x）=1+a，不等式化为 1+a≤x+3，故 x≥a﹣2对 都成立．

故﹣ ≥a﹣2，解得 a≤ ，故a的取值范围为（﹣1， ]．

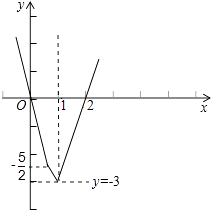
【解析】（1）当a=﹣2时，求不等式f（x）＜g（x）化为|2x﹣1|+|2x﹣2|﹣x﹣3＜0．设y=|2x﹣1|+|2x﹣2|﹣x﹣3，画出函数y的图象，数形结合可得结论．（2）不等式化即 1+a≤x+3，故 x≥a﹣2对 都成立．故﹣ ≥a﹣2，由此解得a的取值范围．
【考点精析】本题主要考查了函数单调性的性质和绝对值不等式的解法的相关知识点，需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集；含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号才能正确解答此题．