题目内容
△ABC的内角A,B,C的对边分别为a,b,c,已知ac=b2-a2,A= ,求B.
,求B.

解析试题分析:首先利用余弦定理将表达式ac=b2-a2进行化简为 b-c=a,然后借助正弦定理将边转化角,利用辅助角公式进行化简求值.
b-c=a,然后借助正弦定理将边转化角,利用辅助角公式进行化简求值.
试题解析:由余弦定理得,a2-b2=c2-2bccosA,
将已知条件代入上式,得ac= bc-c2,则
bc-c2,则 b-c=a,
b-c=a,
再由正弦定理, sinB-sinC=sin
sinB-sinC=sin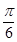 . 4分
. 4分
又sinC=sin( -B)=
-B)= cosB+
cosB+ sinB,
sinB,
所以 sinB-
sinB- cosB=
cosB= ,即sin(B-
,即sin(B-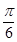 )=
)= . 10分
. 10分
因为-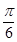 <B-
<B-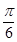 <
< ,所以B-
,所以B-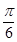 =
=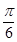 ,即B=
,即B= . 12分
. 12分
考点:1.正弦定理和余弦定理;2.三角化简.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 中,角
中,角 的对边分别为
的对边分别为 .已知
.已知 .
. ;
; ,
, ,且
,且 ,求
,求 .
. ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90°
 ,求PA;
,求PA; 三个内角
三个内角 的对边分别为
的对边分别为 ,向量
,向量 ,
, ,且
,且 与
与 的夹角为
的夹角为 .
. 的值;
的值; ,
, ,求
,求 的值.
的值. 中,其中
中,其中 为定点,
为定点, 为动点,满足
为动点,满足 .
. 与
与 的关系式;
的关系式; 的面积分别为
的面积分别为 和
和 ,求
,求 的最大值,以及此时凸四边形
的最大值,以及此时凸四边形 ,△ABC的面积为2
,△ABC的面积为2 ,求b+c.
,求b+c. ,
, ,
, ,
, ,
, 请你用文字和公式写出计算A、C之间距离的步骤和结果.
请你用文字和公式写出计算A、C之间距离的步骤和结果.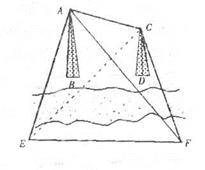
 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且 ,
, 。
。 的值;
的值; 的值。
的值。 的方向追赶渔船乙,刚好用2小时追上。
的方向追赶渔船乙,刚好用2小时追上。
 的值。
的值。