题目内容
设抛物线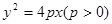
的准线与x轴的交点为
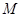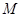，过点作直线
交抛物线于
两点.
(1)求线段
中点的轨迹方程；
(2)若线段的垂直平分线交
轴于
，求证：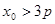
；
(3)若直线的斜率依次取
时，线段的垂直平分线与x轴的交点依次为
，当时
，求
的值.
【答案】
(1) 
(2)见解析
(3) 
【解析】本试题主要是考查了抛物线方程以及抛物线的性质，以及直线与抛物线的位置关系的综合运用，求解中点轨迹方程。并能借助于直线的方程，求解与z轴的交点，并证明坐标构成的等比数列的求和的综合运用
解：（1）抛物线的准线为
，设
代入
得
由
得
设线段
的中点为
，则
消去
，得
即为所求中点的轨迹方程； 4分
（2）
线段的垂直平分线方程为
.
令
,得
;
8分
（3）当斜率
时，
,
是以
为首项，以
为公比的等比数列，且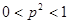
故.
练习册系列答案
相关题目
的准线与x轴交于F1，焦点为F2；以F1，F2为焦点，离心率
的椭圆C2与抛物线C1在x轴上方的交点为P，延长PF2交抛物线于点Q，M是抛物线C1上一动点，且M在P与Q之间运动。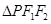
的边长恰好是三个连续的自然数时，求
面积的最大值。
的准线与x轴交于点
,
为焦点，离心率为
的椭圆
与抛物线
在x轴上方的交点为P
交抛物线于点Q,M是抛物线
且P点横坐标为
，求面积
的最大值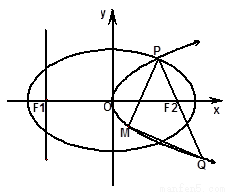
的准线与x轴交于点Q,若过点Q的直线
与抛物线有公共点,则直线