题目内容
对于给定数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得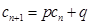 对于任意
对于任意 都成立,我们称数列
都成立,我们称数列 是 “
是 “ 类数列”.
类数列”.
(Ⅰ)若 ,
, ,
, ,数列
,数列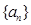 、
、 是否为“
是否为“ 类数列”?若是,指出它对应的实常数
类数列”?若是,指出它对应的实常数 ,若不是,请说明理由;
,若不是,请说明理由;
(Ⅱ)证明:若数列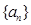 是“
是“ 类数列”,则数列
类数列”,则数列 也是“
也是“ 类数列”;
类数列”;
(Ⅲ)若数列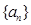 满足
满足 ,
, ,
, 为常数.求数列
为常数.求数列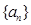 前2012项的和.并判断
前2012项的和.并判断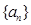 是否为“
是否为“ 类数列”,说明理由.
类数列”,说明理由.
解:(Ⅰ)因为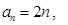 则有
则有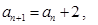

故数列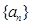 是“
是“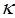 类数列”,对应的实常数分别为
类数列”,对应的实常数分别为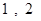 …………… 1分
…………… 1分
因为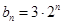 ,则有
,则有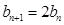 ,
, .
.
故数列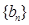 是“
是“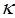 类数列”,对应的实常数分别为
类数列”,对应的实常数分别为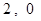 . …………… 3分
. …………… 3分
(Ⅱ)证明:若数列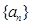 是“
是“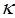 类数列”,则存在实常数
类数列”,则存在实常数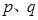 ,
,
使得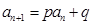 对于任意
对于任意 都成立,
都成立,
且有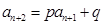 对于任意
对于任意 都成立,
都成立,
因此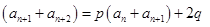 对于任意
对于任意 都成立,
都成立,
故数列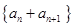 也是“
也是“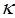 类数列”.
类数列”.
对应的实常数分别为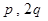 . ……………6分
. ……………6分
(Ⅲ)因为
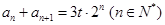 则有
则有 ,
,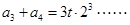 ,
, 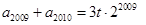
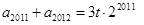
故数列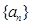 前2012项的和
前2012项的和
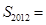
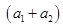 +
+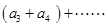 +
+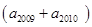 +
+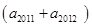
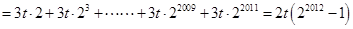 ……………9分
……………9分
若数列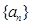 是“
是“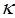 类数列”, 则存在实常数
类数列”, 则存在实常数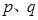
使得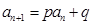 对于任意
对于任意 都成立,
都成立,
且有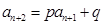 对于任意
对于任意 都成立,
都成立,
因此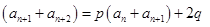 对于任意
对于任意 都成立,
都成立,
而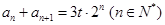 ,且
,且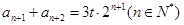 ,
,
则有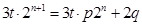 对于任意
对于任意 都成立,可以得到
都成立,可以得到
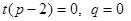 ,
,
当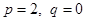 时,
时,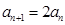 ,
,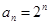 ,
,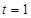 ,经检验满足条件.
,经检验满足条件.
当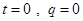 时,
时,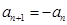 ,
,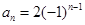 ,
, 经检验满足条件.
经检验满足条件.
因此当且仅当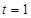 或
或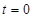 时,数列
时,数列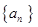 是“
是“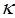 类数列”.
类数列”.
对应的实常数分别为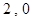 或
或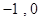 .
………………… 13分
.
………………… 13分
【解析】略

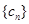 ,如果存在实常数
,如果存在实常数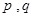 使得
使得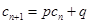 对于任意
对于任意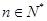 都成立,我们称数列
都成立,我们称数列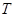 数列”.
数列”.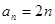 ,
,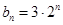 ,
,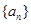 、
、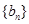 是否为“
是否为“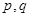 ,若不是,请说明理由;
,若不是,请说明理由;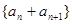 也是“
也是“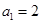 ,
,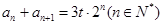 ,
,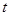 为常数.求数列
为常数.求数列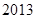 项的和.
项的和.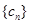 ,如果存在实常数
,如果存在实常数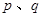 ,使得
,使得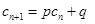 对于任意
对于任意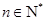 都成立,我们称数列
都成立,我们称数列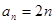 ,
,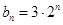 ,
,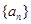 、
、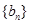 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数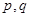 ,若不是,请说明理由;
,若不是,请说明理由;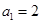 ,
, .
.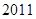 项的和.
项的和.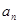 .
. ,如果存在实常数
,如果存在实常数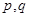 ,使得
,使得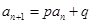 对于任意
对于任意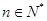 都成立,我们称数列
都成立,我们称数列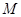 类数列”.
类数列”.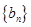 是 “
是 “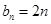 ,求它对应的实常数
,求它对应的实常数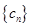 满足
满足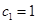 ,
,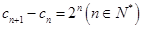 ,求数列
,求数列 ,如果存在实常数
,如果存在实常数 ,使得
,使得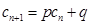 对于任意
对于任意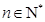 都成立,我们称数列
都成立,我们称数列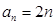 ,
,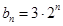 ,
,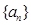 、
、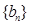 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数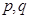 ,若不是,请说明理由;
,若不是,请说明理由;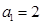 ,
, .
.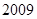 项的和.(2)已知数列
项的和.(2)已知数列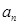 .
.