题目内容
（2011•宁波模拟）如图，△ABC中，| GA |
| GB |
| GC |
| O |
| CA |
| a |
| CB |
| b |
| CP |
| a |
| CQ |
| b |
| CG |
| CH |
| 1 |
| m |
| 1 |
| n |
分析：由△ABC中，
+
+
=0，知G是△ABC的重心，由
=
，
=
，
=m
，
=n
，CG∩PQ=H，
=2
，假设QP∥AB，过G点作EF∥PQ，交AC于E，交BC于F，由重心的性质知m=n=
，由此能求出
+
的值．
| GA |
| GB |
| GC |
| CA |
| a |
| CB |
| b |
| CP |
| a |
| CQ |
| b |
| CG |
| CH |
| 1 |
| 3 |
| 1 |
| m |
| 1 |
| n |
解答：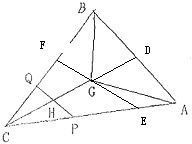
解：∵△ABC中，
+
+
=0，
∴G是△ABC的重心，
∵
=
，
=
，
=m
，
=n
，CG∩PQ=H，
=2
，
由平行线等分线段成比例定理，可以取特殊值，
假设QP∥AB，过G点作EF∥PQ，交AC于E，交BC于F，
延长CG交AB于D，
∴PQ∥EF∥AB，
∵
=2
，
由重心的性质知：
CH=HG=DG，
∵PQ∥EF∥AB，
∴CQ：QF：FB=CH：HG：GD=CP：PE：EA，
∴m=n=
，
∴
+
=6．
故选C．
解：∵△ABC中，| GA |
| GB |
| GC |
∴G是△ABC的重心，
∵
| CA |
| a |
| CB |
| b |
| CP |
| a |
| CQ |
| b |
| CG |
| CH |
由平行线等分线段成比例定理，可以取特殊值，
假设QP∥AB，过G点作EF∥PQ，交AC于E，交BC于F，
延长CG交AB于D，
∴PQ∥EF∥AB，
∵
| CG |
| CH |
由重心的性质知：
CH=HG=DG，
∵PQ∥EF∥AB，
∴CQ：QF：FB=CH：HG：GD=CP：PE：EA，
∴m=n=
| 1 |
| 3 |
∴
| 1 |
| m |
| 1 |
| n |
故选C．
点评：本题考查平面向量的综合应用，是基础题．解题时要认真审题，解题的关键是由
+
+
=0，知G是△ABC的重心．然后取特殊值假设QP∥AB，能够又快又准地得到答案．
| GA |
| GB |
| GC |
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目