题目内容
某班植树小组栽培甲、乙两种松树,已知小组中每位成员甲、乙两种至少要栽培一种,已知栽培甲品种的有2人,栽培乙品种的有6人,现从中选2人,设选出的人中既栽培甲品种又栽培乙品种的人数为ξ,且P(ξ=0)=
,求:
(1)植树小组的人数;
(2)随机变量ξ的数学期望.
| 2 | 5 |
(1)植树小组的人数;
(2)随机变量ξ的数学期望.
分析:(1)设植树小组共有x人,两品种均栽培的有(8-x)人,则恰栽一品种的人数为(2x-8)人,利用P(ξ=0)=
,建立方程,即可求得植树小组的人数;
(2)先确定恰栽一品种的有4人,两品种均栽培的有2人,计算ξ=1,2时的概率,即可求得数学期望.
| 2 |
| 5 |
(2)先确定恰栽一品种的有4人,两品种均栽培的有2人,计算ξ=1,2时的概率,即可求得数学期望.
解答:解:(1)设植树小组共有x人,两品种均栽培的有(8-x)人,则恰栽一品种的人数为(2x-8)人…(2分)
∵P(ξ=0)=
,∴
=
…(4分)
整理为:3x2-28x+60=0,∴x=6,即植树小组有6人…(6分)
(2)依(1)有:恰栽一品种的有4人,两品种均栽培的有2人
P(ξ=1)=
=
…(8分);P(ξ=2)=
=
…(10分)
∴Eξ=0×
+1×
+2×
=
…(12分)
∵P(ξ=0)=
| 2 |
| 5 |
| ||
|
| 2 |
| 5 |
整理为:3x2-28x+60=0,∴x=6,即植树小组有6人…(6分)
(2)依(1)有:恰栽一品种的有4人,两品种均栽培的有2人
P(ξ=1)=
| ||||
|
| 8 |
| 15 |
| ||
|
| 1 |
| 15 |
∴Eξ=0×
| 2 |
| 5 |
| 8 |
| 15 |
| 1 |
| 15 |
| 2 |
| 3 |
点评:本题考查离散型随机变量的概率与期望,解题的关键是正确求出概率,利用期望公式求解.

练习册系列答案
相关题目
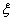 ,且
,且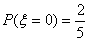 ,求:
,求: