题目内容
已知圆O: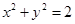 交
交 轴于A,B两点,曲线C是以
轴于A,B两点,曲线C是以 为长轴,离心率为
为长轴,离心率为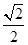 的椭圆,其左焦点为F.若P是圆O上一点连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
的椭圆,其左焦点为F.若P是圆O上一点连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
(1)求椭圆C的标准方程;
(2)若点P的坐标为(1,1),求证:直线PQ与圆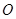 相切;
相切;
(3)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
解:(1)椭圆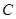 的标准方程为
的标准方程为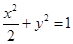
(2)因为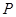 (1,1),所以
(1,1),所以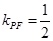 ,所以
,所以 ,所以直线OQ的方程为y=-2x
,所以直线OQ的方程为y=-2x
又椭圆的左准线方程为x=-2,所以点Q(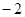 ,4)
,4)
所以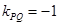 ,又
,又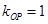 ,所以
,所以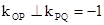 ,即
,即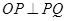 ,故直线
,故直线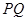 与圆
与圆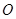 相切
相切
(3)当点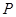 在圆
在圆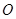 上运动时,直线
上运动时,直线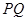 与圆
与圆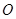 保持相切
保持相切
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
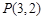 ,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程.
,焦点在坐标轴上,长轴长是短轴长的3倍,求该椭圆的方程. 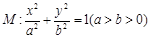 的离心率为
的离心率为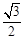 ,直线
,直线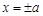 和
和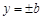 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.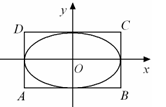
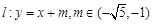 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点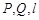 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点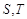 .求
.求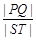 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.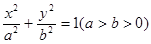 的离心率
的离心率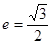 ,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且
,A,B分别为椭圆的长轴和短轴的端点,M为AB的中点,O为坐标原点,且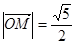 .
.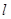 交椭圆于P,Q两点,求△POQ面积最大时直线
交椭圆于P,Q两点,求△POQ面积最大时直线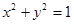 过椭圆
过椭圆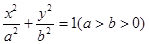 的两焦点,与椭圆有且仅有两个公共点;直线
的两焦点,与椭圆有且仅有两个公共点;直线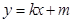 与圆
与圆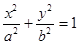 相交于
相交于 两点记
两点记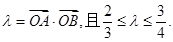
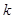 的取值范围;
的取值范围;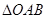 的面积S的取值范围.
的面积S的取值范围.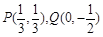 ;
;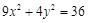 具有共同的焦点.
具有共同的焦点.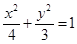 的中心,焦点与该椭圆的右焦点重合。
的中心,焦点与该椭圆的右焦点重合。 ,点O为坐标原点,一条直线
,点O为坐标原点,一条直线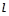 :
: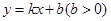 与圆O相切并与椭圆
与圆O相切并与椭圆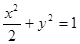 交于不同的两点A、B
交于不同的两点A、B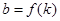 ,求
,求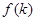 的表达式;
的表达式; 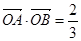 ,求直线
,求直线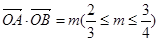 ,求三角形OAB面积的取值范围.
,求三角形OAB面积的取值范围.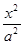 -
-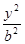 =1(
=1(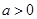 ,
,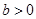 )的一个焦点,如果抛物线与双曲线交于
)的一个焦点,如果抛物线与双曲线交于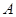 (
(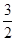 ,
,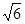 ),
),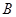 (
(