题目内容
对于每一个实数x,设函数f(x)是y=4x+1,y=x+2,y=-2x+4三个函数中的最小值,则f(x)的最大值是 .
【答案】分析:先求出每2条直线的交点坐标,利用函数f(x)是y=4x+1,y=x+2,y=-2x+4三个函数中的最小值,写出f(x)的解析式,结合f(x)的图象求出f(x)的最大值.
解答:解:由y=4x+1和y=x+2联立方程组,解得两直线的交点( ,
, ),
),
由 y=x+2和y=-2x+4联立方程组,解得两直线的交点( ,
, ),
),
由y=4x+1和 y=-2x+4联立方程组,解得两直线的交点( 3),
3),
∵函数f(x)是y=4x+1,y=x+2,y=-2x+4三个函数中的最小值,
∴f(x)=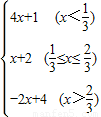 ,
,
∴x= 时,f(x)有最大值是
时,f(x)有最大值是  ,
,
故答案为 .
.
点评:本题考查函数最值及其几何意义,体现分类讨论的数学思想.
解答:解:由y=4x+1和y=x+2联立方程组,解得两直线的交点(
 ,
, ),
),由 y=x+2和y=-2x+4联立方程组,解得两直线的交点(
 ,
, ),
),由y=4x+1和 y=-2x+4联立方程组,解得两直线的交点(
 3),
3),∵函数f(x)是y=4x+1,y=x+2,y=-2x+4三个函数中的最小值,
∴f(x)=
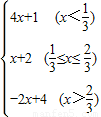 ,
,∴x=
 时,f(x)有最大值是
时,f(x)有最大值是  ,
,故答案为
 .
.点评:本题考查函数最值及其几何意义,体现分类讨论的数学思想.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目