题目内容
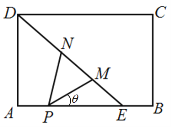
【题目】【2017广东佛山二模】如图,矩形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 在
在![]() 边上,且
边上,且![]() ,将
,将![]() 沿
沿![]() 折到
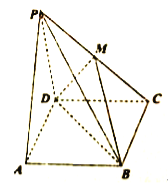
折到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() .
.
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.

【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】试题分析:(I)连接![]() 交
交![]() 于点
于点![]() ,根据对应边成比例可证得两个直角三角形
,根据对应边成比例可证得两个直角三角形![]() 相似,由此证得
相似,由此证得![]() ,而
,而![]() ,故
,故![]() 平面
平面![]() ,所以
,所以![]() .(II)由(I)知
.(II)由(I)知![]() 平面
平面![]() ,以
,以![]() 为原点联立空间直角坐标系,利用平面
为原点联立空间直角坐标系,利用平面![]() 和平面
和平面![]() 的方向量,计算两个半平面所成角的余弦值.
的方向量,计算两个半平面所成角的余弦值.
试题解析:
(Ⅰ)连接![]() 交
交![]() 于点
于点![]() ,依题意得
,依题意得![]() ,所以
,所以![]()
![]() ,
,
所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
即![]() ,
, ![]() ,又
,又![]() ,
, ![]() ,
,![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() .
.
(Ⅱ)因为平面![]() 平面
平面![]() ,
,
由(Ⅰ)知, ![]() 平面
平面![]() ,
,
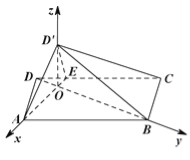
以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() 如图所示.
如图所示.
在![]() 中,易得
中,易得![]() ,
, ![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,
, ![]() ,
,
设平面![]() 的法向量
的法向量![]() ,则
,则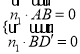 ,即
,即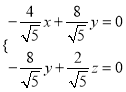 ,解得
,解得![]() ,
,
令![]() ,得
,得![]() ,
,
显然平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以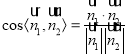
![]() ,所以二面角
,所以二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】某公司2005~2010年的年利润x(单位:百万元)与年广告支出y(单位:百万元)的统计资料如表所示:
年份 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
利润x | 12.2 | 14.6 | 16 | 18 | 20.4 | 22.3 |
支出y | 0.62 | 0.74 | 0.81 | 0.89 | 1 | 1.11 |
根据统计资料,则( )
A.利润中位数是16,x与y有正线性相关关系
B.利润中位数是18,x与y有负线性相关关系
C.利润中位数是17,x与y有正线性相关关系
D.利润中位数是17,x与y有负线性相关关系